1. 서 론

최근 신·재생에너지 중 태양광발전 시스템은 기술적 진보와 급격한 시장의 성장으로 급속도로 확대되고 있다. 태양광발전 시스템은 태양의 빛 에너지를 전기 에너지로 전환시키는 발전의 특성으로 외부 환경에 노출되어야 한다. 따라서 태양광발전 시스템은 외부 환경에서 내부 고장 또는 성능저하 없이 시스템의 성능과 품질을 유지하는 것이 중요하다¹⁾.

전 세계는 심각한 이상기후 현상으로 살인 더위, 우박 폭풍, 기록적 폭우 등 인명피해가 속출하고 있다. 인명피해 뿐만 아니라 재산피해 역시 증가하고 있다. 강력한 우박 폭풍은 태양광모듈에 심각한 문제를 발생시킬 수 있다. 우박 충돌로 인한 태양광모듈의 피해는 전면 유리를 파손시키는 1차 피해가 있고 태양광모듈 내 실리콘 태양전지의 미세균열(micro-crack)을 발생시키는 2차 피해가 있다. 1차 피해는 육안으로 확인이 가능하나 2차 피해인 태양전지의 미세균열은 육안으로 확인이 어렵고 즉시 피해(발전 손실)를 확인하는 것은 더욱 어렵다. 미세균열은 electroluminescence (EL)와 열화상 측정 장치로 확인이 가능하나 지붕 태양광발전 설비같이 측정자와 측정 장비의 접근성이 떨어지는 곳에서는 확인이 어렵다. 이러한 문제점은 열화상 카메라가 장착된 드론을 이용한 방법으로 해결이 가능하지만 측정 위치의 낮은 정밀도와 해상도 문제가 있다.

IEC 61215는 결정질 실리콘 태양광모듈의 건전성 평가를 위한 국제규격이다²⁾. IEC 61215의 우박 시험(Hail test)은 태양광모듈이 얼음 충격에 견딜 수 있는지 검증하는 것이 목적이다. 절차는 다음과 같다. 우박 시험은 일정 지름을 갖는 얼음을 규정 속도로 태양광모듈에 발사하여 타격 영역의 손상에 대하여 현저한 육안 결함이 없어야 하며 우박 시험 이전 출력 저하가 5%를 초과해서는 안 된다. 우박 충돌에 의한 태양광모듈의 손상, 전력 손실, 경제적 피해 등에 관한 문헌들이 보고되어 왔다^3,4). 우박 충돌에 의한 태양광모듈의 전력 손실에 대한 연구동향을 살펴보면 Dolara et al⁵⁾은 미세 균열이 태양광모듈의 전력 생산량을 29% 감소시킨다고 보고하였다. Dhimish⁶⁾는 미세 균열이 발생된 4000개의 실리콘 태양전지를 분석하였다. 그는 미세 균열이 0.9 ~ 42.8 % 태양광모듈의 출력을 저하시키며 핫스팟에도 상당한 상관관계가 있다고 주장하였다. 균열이 발생된 태양전지 내에 약 7.6℃ 이상의 열이 발생되면 태양전지에 영구적인 핫스팟이 발생될 수 있다고 주장한다. 이와 같이 우박 충돌로 발생한 태양광모듈 내 미세 균열은 태양광발전 성능 및 기대 수명을 감소시키기 때문에 우박 충돌로부터 태양광모듈의 건전성 확보는 반드시 필요한 연구 분야이다. 우박 충돌로 발생 가능한 미세균열 같은 결함을 찾는 것은 실제 실험적 분석보다 시뮬레이션 분석이 경제적으로 우수하다. Makaraskas et al⁷⁾은 실리콘 태양광모듈과 우박 충돌을 시뮬레이션으로 구현하였다. 그들은 전면 유리와 태양광모듈 내 봉지재(EVA, ethylene vinyl acetate) 상부와 하부의 두께를 변화시켜 우박 충돌과정에서 발생한 충격이 태양전지에 미치는 응력을 관찰하였다. 하지만 다양한 우박 충돌 조건에 대한 연구가 이루어지지 않고 있어서 우박 충돌에 대한 태양광모듈의 건전성을 평가하는 연구가 부족한 상태이다.

본 논문은 IEC 기준에 따라 우박 시험 조건을 충돌 해석 프로그램으로 구현하였고 태양광모듈의 전면 유리 두께를 변화하여 충돌 해석을 수행하였다. 우박 충돌 시 얼음 입자의 거동이 태양광모듈에 미치는 영향을 분석하여 태양광모듈의 건전성을 평가하고자 한다.

2. 우박 충돌 해석

2.1 우박 충돌 해석 모델

우박은 구형의 얼음 입자로 구현하였는데 얼음은 온도, brine 함유율, 결정의 크기, 변형률 등 다양한 요소들에 의해 변형된다^8,9,10). 본 연구에서 얼음은 부서지기 쉬운 물질(brittle material)이며 구형의 형상으로 온도는 -20℃ 설정하였다. 얼음 입자는 ANSYS workbench의 engineering data에서 제공하는 물을 사용하고 참고문헌의 물성 값과 모델을 추가하였다. 얼음 입자의 상태방정식은 EOS, Strength 모델은 Johnson cook, Failure 모델은 Principal stress를 적용하였다^11,12,13).

태양광모듈은 다양한 재료로 구성되는데 본 연구는 태양광모듈의 구성요소를 유리, 봉지재, 실리콘 태양전지, 그리고 봉지재 순서로 단순화하였다. 태양광모듈을 고정하는 알루미늄 프레임은 제외하였다. 태양광모듈 내 백시트는 우박 충돌시 구조적 강도를 향상시키는 역할을 하지만 본 연구에서는 제외하였다. 전면유리는 soda-lime glass로 정하고 참고문헌의 물성 값을 사용하였다14). 봉지재는 polyurethane, 실리콘 태양전지는 silicon carbide로 정하였고 ANSYS workbench의 engineering data에서 제공하는 물성 값을 사용하였다11). 충돌 해석에 사용한 재료의 물성 값과 모델은 Table 1부터 4까지 정리하였다. 충돌 해석은 부서지기 쉬운 물질의 충돌 해석을 위해 유한요소를 사용하지 않는 SPH (Smoothed Particle Hydrodynamics) 방법을 적용하였다. 이 방법은 요소 왜곡현상이 발생하지 않아 입자의 충돌 해석의 정확도가 높다11). 태양광모듈은 라그랑지안 기법으로 유한 요소 모델링을 수행하였다. 해석의 단순화로 인해 모듈 구성부품의 변형률에 차이가 발생될 수 있으나 우박 충돌에 따른 실리콘 태양전지의 미세균열 경향을 분석하는데 있어 큰 영향이 없을 것으로 판단된다.

2.2 우박 충돌 해석 검증

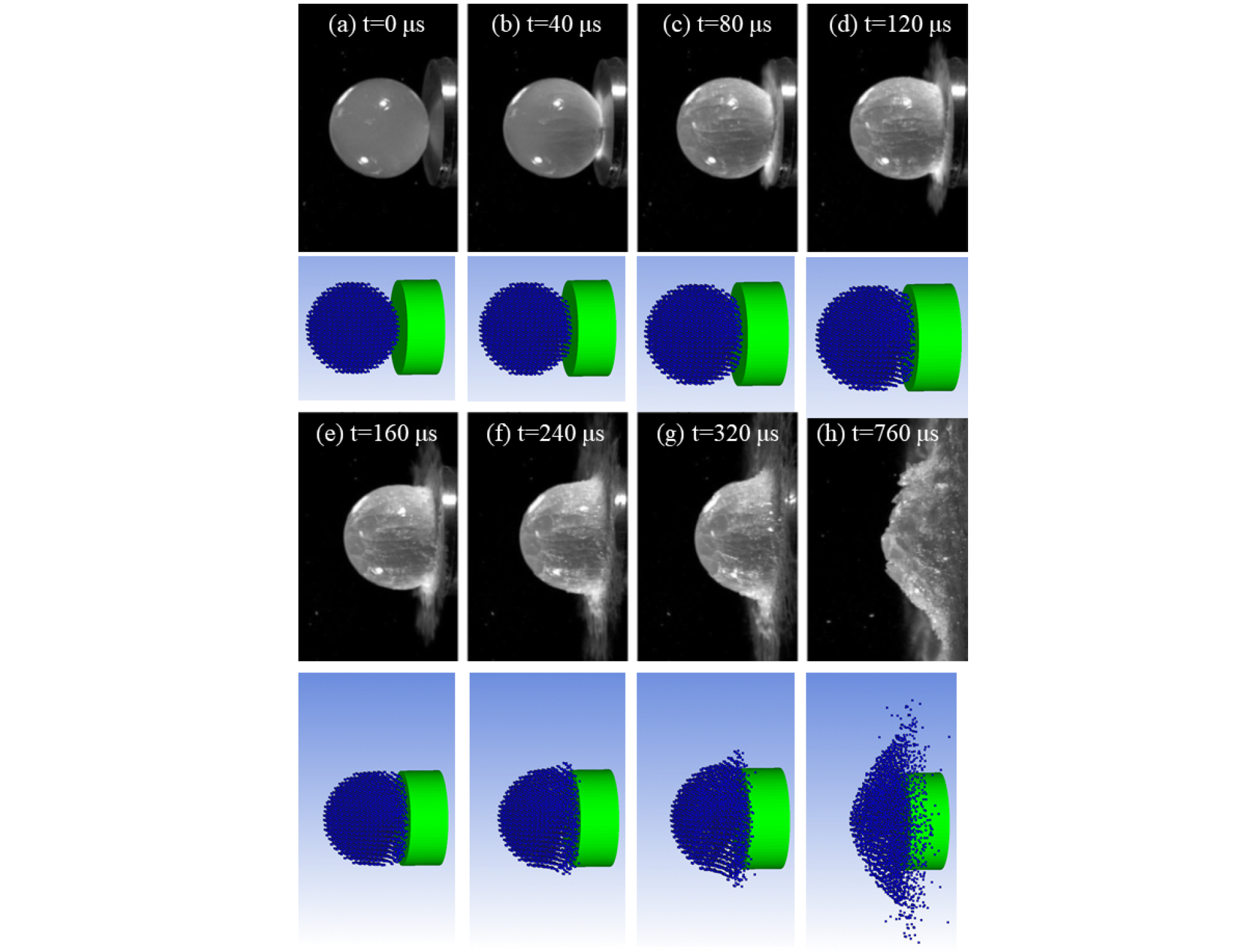
본 연구에 적용된 해석 방법의 적합성을 검증하기 위해 우박 충돌 실험에서 사용한 충돌 과정을 비교하였다12). 얼음 입자 충돌 실험은 61.0 mm 직경을 갖는 얼음 입자를 61.8 m/s의 속도로 알루미늄 기판에 충돌하는 과정을 초고속 촬영한 결과이다. 모델 검증을 위한 충돌 해석은 얼음 입자 충돌 시험과 동일하게 모사하였다. 얼음 입자의 직경은 61.0 mm이고 입자의 속도는 61.8 m/s로 설정하였다. 충돌 기판의 재료는 Aluminum 6061-T6으로 실험과 동일한 재질이고 출돌 기판의 직경은 입자와 동일한 크기를 사용하였다. 모델 검증을 위한 충돌 해석은 표1과 표5에 재료의 물성 값과 모델을 정리하였다. Fig. 1은 검증 모델의 입자의 거동과 실험의 얼음 입자의 거동 과정이 유사함을 보였다. 따라서 본 연구에서 사용한 우박 충돌 해석 방법은 적절한 것으로 판단된다.

Fig. 1.

Validation of ice particle impacting aluminum substrate¹²⁾ With permission from Elsevier

2.3 우박 충돌 해석 조건

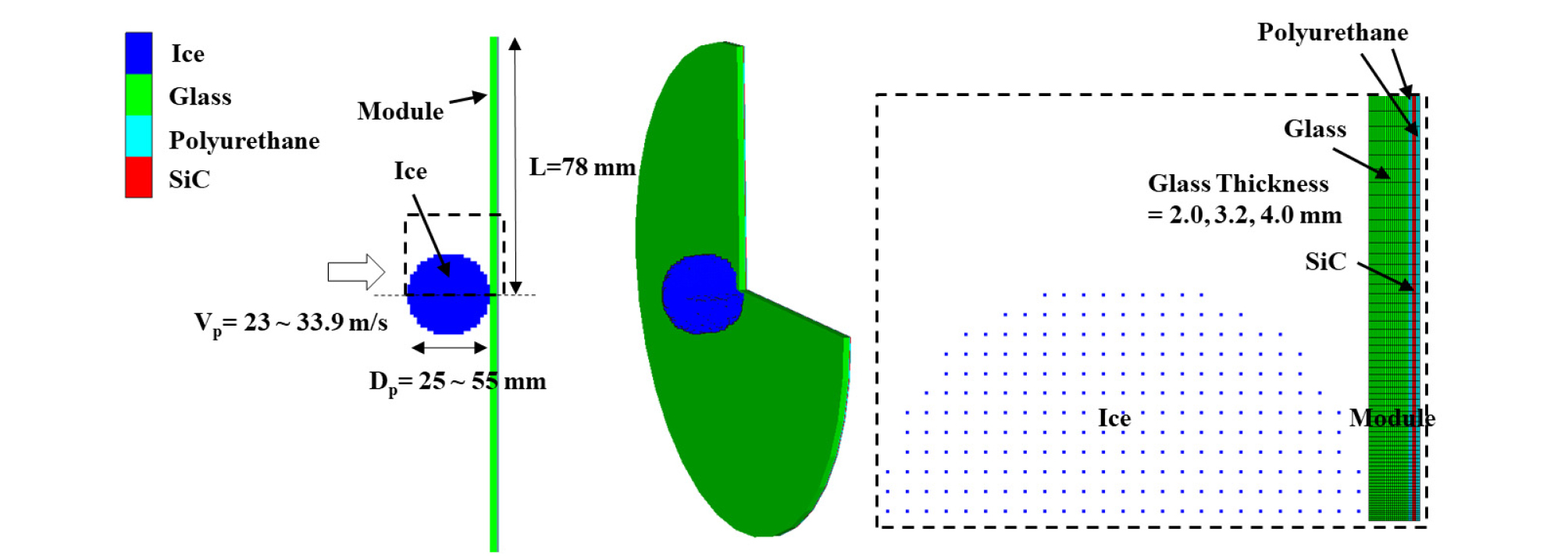
IEC 61215 우박 시험과 동일하게 전산해석 모델링을 수행하였다. 충돌 해석은 전산해석에 소요되는 시간과 비용을 최소하화기 위해 2차원 축대칭 형태로 얼음 입자와 태양광모듈에 대한 모델링을 수행하였다. 충돌 해석에서 태양광모듈은 유리 기판, 봉지재, 실리콘 태양전지, 봉지재 순으로 각 층을 이루고 있으며 라그랑지안 요소로 모델링하였다. 태양광모듈을 구성하는 각 층은 완전 접촉(노드 공유)되어 있어 동일한 변형량을 갖도록 설계하였다. 태양광모듈의 형상은 원판으로 가정하였고 구성요소는 4절점의 사각형 요소로 격자를 생성하였다. Fig. 2와 같이 격자수는 2,842개 (얼음 입자 242개, 모듈 2,600개)로 이루어져 있다. 유리 기판의 두께가 증가할수록 모듈의 격자수도 비례하여 증가시켰다. 얼음 입자의 격자 역시 242에서 1,185개로 직경의 증가에 비례하여 격자수를 증가하였다. 얼음 입자의 충돌 방향은 태양광모듈 내 실리콘 태양전지의 중앙으로 설정하였다. 얼음 입자 충돌 시뮬레이션은 IEC 기준에 근거하여 Table 6과 같이 선정하였다. 전면 유리 두께는 얼음 입자의 충돌과정에서 발생하는 태양광모듈 내부의 미세균열을 관찰하기 위해 설계되었다. 규격화된 태양광모듈(1600 × 980 mm²)의 중량 중 전면유리가 전체 태양광모듈의 약 65% 이상을 차지한다15). 따라서 전면유리 두께는 태양광모듈의 건전성에 밀접한 관계가 있기 때문에 다양한 두께에 대한 충돌 해석을 수행하였다. 본 연구에서 태양광모듈 내 태양전지의 파손은 변형률이 15% 이상의 경우로 가정하였는데 이는 Yoon et al.16)에서 가정한 구성품의 파손 가정과 동일하게 적용하였다.

Fig. 2.

Hail impact modelling

3. 해석 결과

3.1 입자의 거동

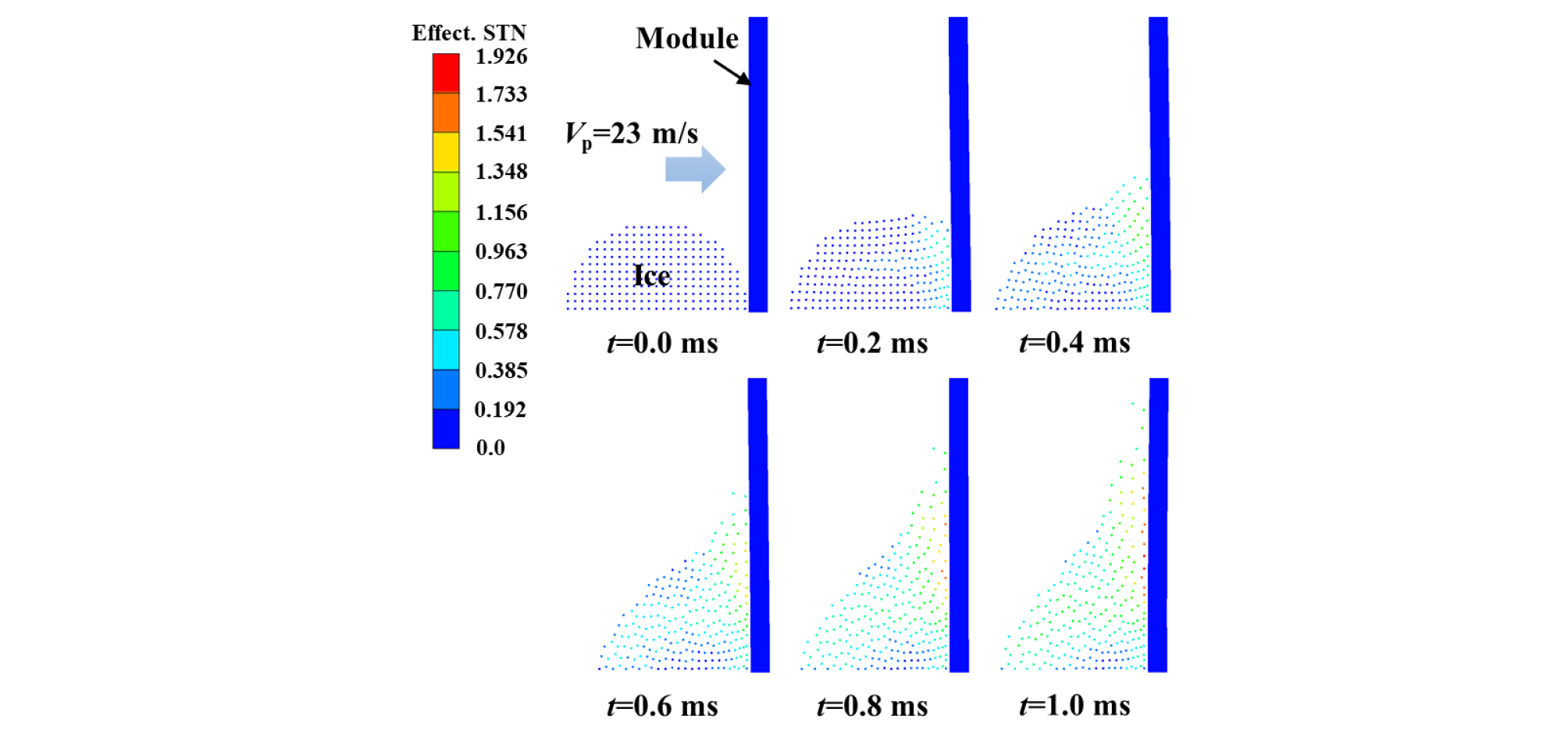
Fig. 3은 1.99 J의 운동에너지를 갖는 얼음 입자가 유리 두께가 2.0 mm인 태양광모듈에 충돌하는 과정을 시간대별로 나타낸 결과이다. 충돌 결과는 충돌 초기 입자의 형상유지, 입자의 국부적 파쇄, 입자의 이동방향에 대한 종방향으로 분산과정 등 얼음 입자의 균열과정이 명확히 관찰된다12). 특히, 충돌 후 t=0.4 ms에서 얼음 입자는 충돌 면에서 분쇄와 입자의 균열 과정이 관찰되었다. 충돌 후 t=0.6 ms 이후 얼음 입자의 원형은 남아 있지 않고 종방향으로 흩뿌려지는 분산 과정이 관찰되었다.

Fig. 3.

Effective strain contours and progress of hail impaction on module

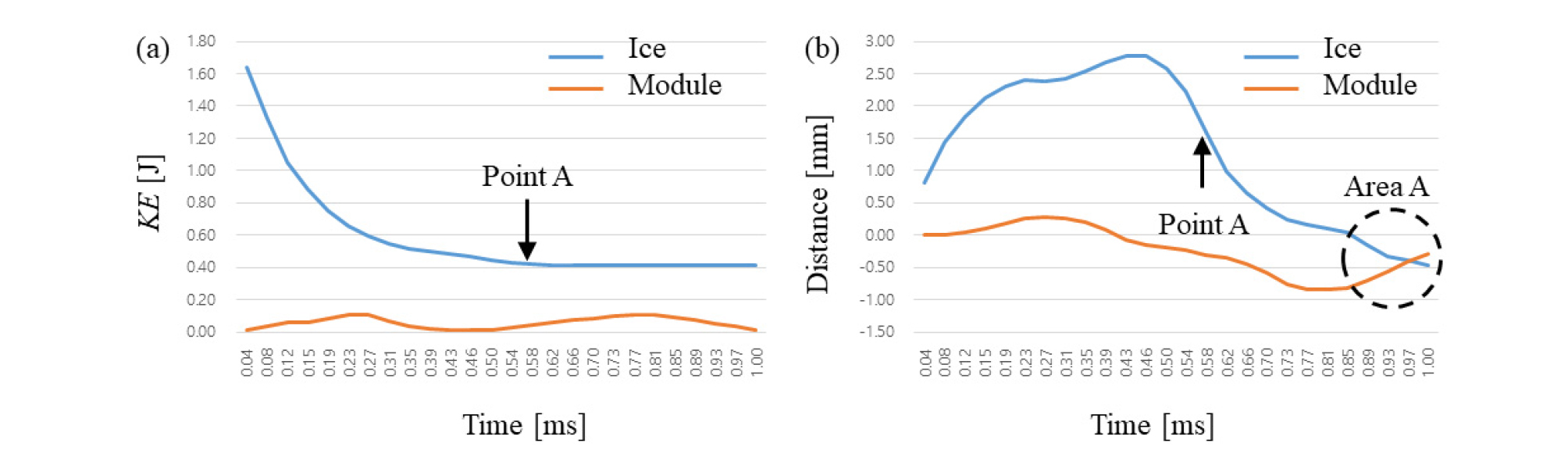
Fig. 4는 Fig. 3의 충돌 시뮬레이션 결과를 시간의 변화에 따른 운동에너지와 이동거리의 변화로 나타냈다. 얼음 입자의 운동에너지는 태양광모듈과 충돌하여 점차 감소한다. 반대로 태양광모듈의 운동에너지는 정적인 상태에서 얼음 입자의 충돌로 인해 증가하다 감소한다. 이것은 입자의 운동에너지가 태양광모듈에 전달되어 모듈 내부로 충격량을 흡수하기 때문이다. Fig. 4(a)와 (b)에서 Point A(A 지점)는 얼음 입자의 운동에너지가 일정하게 유지되는 완전침투(full penetration)가 발생되는 지점이다. A 지점 이후 모듈은 충돌에 의해 이동된 거리에서 원위치로 되돌아오는 것을 확인할 수 있다. Area A(A 영역)는 모듈의 되돌아오는 과정으로 얼음과 모듈의 이동거리가 음(-)으로 표기된다. 또한 태양광모듈 내부 실리콘 태양전지는 충돌과정에서 변형률의 변화가 관찰되지 않아 파손이 발생되지 않았다.

Fig. 4.

(a) Kinetic energy-time curve, (b) Penetration distance-time curve of ice and module

3.2 모듈 외부 파손

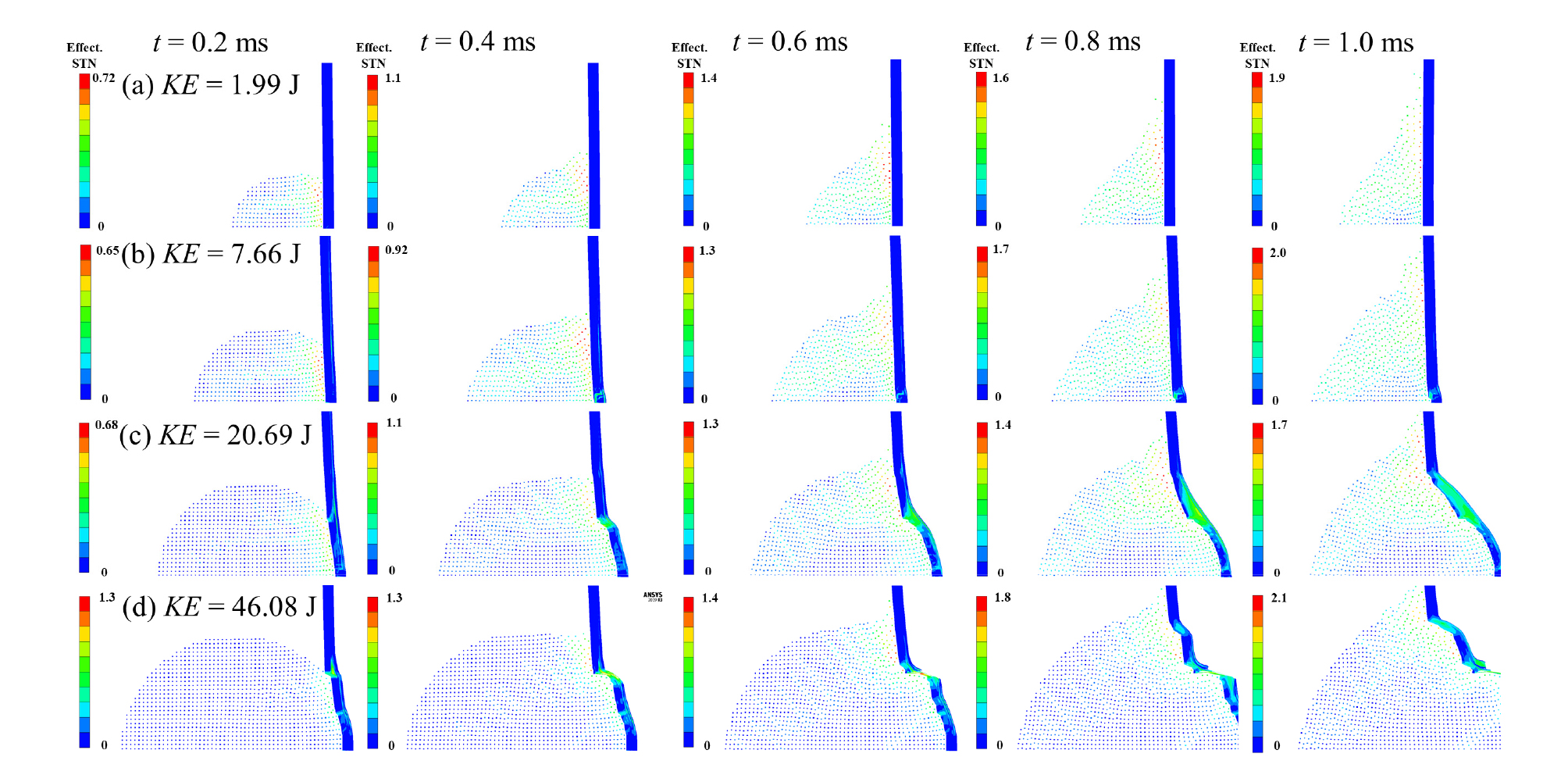
Fig. 5는 운동에너지의 증가가 태양광모듈에 미치는 영향을 시간대별로 정리한 결과이다. 운동에너지는 1.99, 7.66, 20.69, 46.08 J로 점차 증가하였고 태양광모듈의 유리 두께는 2.0 mm로 고정하였다. Fig. 3과 4에서 정리하였듯이 운동에너지가 1.99 J인 경우는 태양광모듈 전체에 영향이 없다. 그러나 운동에너지가 7.66 J 이상이 모든 경우에서는 태양광모듈의 변형률이 증가가 관찰되었다. 특히 운동에너지가 20.69와 46.08 J인 경우 태양광모듈의 심각한 변형과 손상이 발생되었고 시간이 증가함에 따라 변형과 손상의 범위가 증가하였다. 태양광모듈의 유리 두께가 입자의 운동에너지를 충분히 흡수하지 못하여 얼음 입자 충돌 시 태양광모듈의 변형 및 파괴현상이 수반되었다.

Fig. 5.

Effective strain contours and increasing KE at different impact times on 2.0 mm glass thickness module

3.3 모듈 내부 파손

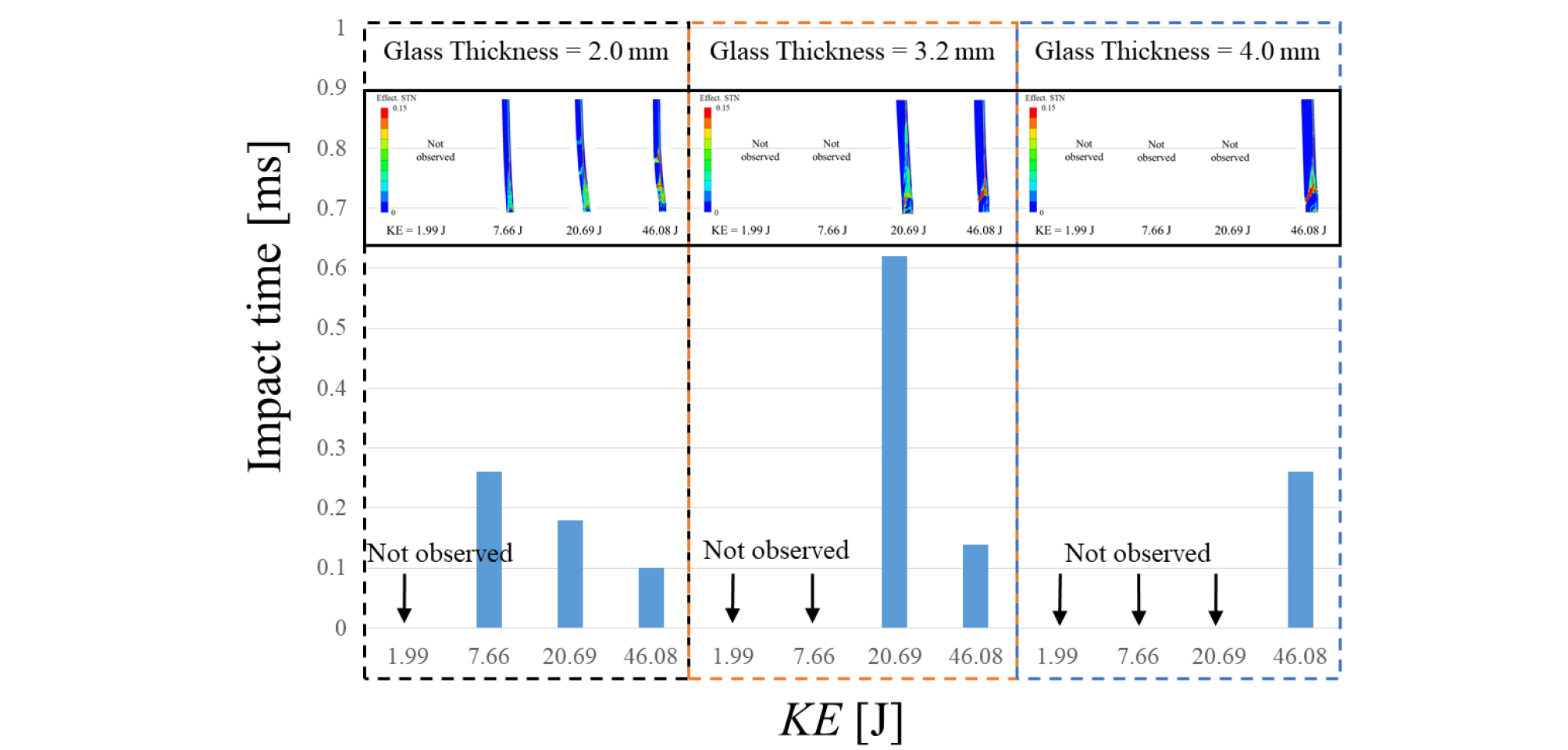
Fig. 6은 얼음 입자의 운동에너지와 유리 두께 변화에 따라 충돌 후 태양광모듈 내부 실리콘 태양전지의 변형률 변화를 관찰한 결과이다. 실리콘 태양전지의 변형률이 15% 이상일 경우 파손 되었다고 가정하였고 충돌 후 소요되는 시간을 확인하였다. Fig. 6에 삽입된 이미지는 태양전지의 파손이 일어난 해당 시간에서의 변형률을 나타낸 결과이다. 2.0 mm의 유리 두께를 갖는 태양광모듈은 얼음의 운동에너지가 1.99 J의 경우를 제외하고 모두 파손되었다. 특히 충돌 후 0.3 ms 이내에 모두 파손되었다. 유리 두께가 증가한 3.2와 4.0 mm의 태양광모듈들은 7.66 J의 운동에너지를 갖는 얼음에 대해서 모두 안정적이었다. 다만 46.08 J의 운동에너지에 대해서 모든 태양광모듈은 내부 파손이 발생되었다. 유리 두께의 증가는 얼음 입자의 운동에너지 변화에 따라 실리콘 태양전지 내부의 파손을 감소시켰다. 태양광모듈의 전면유리는 얼음 입자와 충돌 시 얼음 입자의 운동에너지를 완충시켜 실리콘 태양전지의 내부 파손을 최소화시킨다. 태양광모듈의 유리 두께의 증가가 충돌 시 발생한 운동에너지의 완충 효과가 반영되어 나타난 결과로 추정한다. 따라서 4.0 mm의 유리 두께를 갖는 태양광모듈이 얼음 입자 충돌에서 내구성이 우수한 결과를 보였다. 이러한 결과는 다른 문헌의 결과와 일치한다. Mathiak et al.17)은 우박 충돌에 대한 연구실 실험과 현장 경험을 바탕으로 전면 유리의 파손은 50 mm 직경의 얼음 입자가 태양광모듈 프레임 근처에 충돌할 경우 태양광모듈 유리의 파손이 발생되었다고 보고하였다. 특히 3.2 mm 보다 두꺼운 4.0 mm의 유리 두께를 갖는 태양광모듈이 우박 충돌에 더 잘 견딘다고 보고하였다. 유리 두께의 증가는 태양광모듈의 건전성에 있어 우수하지만 경제성과 밀접한 관련이 있고 태양광모듈 무게 증가에 큰 요소로 작용되기 때문에 최적의 유리 두께 선정이 중요하다.

Fig. 6.

Internal damage results of silicon solar cells with different glass thickness

4. 결 론

본 연구는 IEC 61215에서 수행하는 태양광모듈의 신뢰성 평가 중 우박 시험을 전산해석으로 모사하여 실리콘 태양광모듈 내부 미세균열을 평가하였다. 충돌 해석은 경계조건을 단순화하여 수행하였기 때문에 실제 우박 시험과 동일한 결과로 볼 수 없으나 우박 충돌에 대한 연구실 실험과 현장 사례에서 나타나는 결과와 해석 결과는 유사함을 보였다. 충돌 해석은 얼음 입자의 운동에너지와 태양광모듈을 보호하는 유리 두께를 대상으로 수행하였고 얼음 입자 충돌과정에서 발생되는 입자의 거동과 태양광모듈의 외부 파손을 관찰하였다. 또한 태양광모듈의 유리 두께의 변화가 얼음 입자 충돌 시 발생되는 모듈 내 실리콘 태양전지의 파손 여부를 분석하였다. 연구 결과는 우박 시험 결과를 통해 직접적인 모듈 파손여부 뿐만 아니라 육안으로 확인이 어려운 태양광모듈 내 실리콘 태양전지의 미세균열을 관측하고 예측하는데 활용이 가능하다. 따라서 새로운 형태의 태양광모듈에 대한 신뢰성 및 정밀 분석에 활용하여 신뢰성 평가를 위한 시간을 단축 가능할 것으로 판단된다. 충돌 해석 결과향후, 실제 태양광모듈이 설치장소를 기반으로 전산해석 연구를 추가적으로 수행하여 기후 변화로 인해 가혹한 조건(우박의 직경 증가 등)에서 장기 신뢰성을 갖는 태양광모듈에 대한 연구를 수행하고자 한다.

기호설명

KE : 운동에너지 (J)
t : 충돌 시간
V_p : 입자의 속도 (m/s)
D_p : 입자의 직경 (mm)