1. 서 론
2. 와이블 분포(Weibull distribution)
3. 풍속 데이터
3.1 측정 풍속 데이터
3.2 가상 풍속 데이터
4. 확률도시위치 공식의 Lnleast 방법 적용
4.1 Lnleast 방법(Ln-least method)
4.2 확률도시위치(PPP: probability plotting position) 공식의 적용
5. 확률도시위치 적용 시 Lnleast 방법의 예측 정확도 비교
5.1 정확도 검사 방법
5.2 정확도 검사 결과
6. 결 론
1. 서 론
바람은 보통 계절에 따라 주기적으로 변하며, 특정 지역에서 일정 기간(보통 1년 이상) 동안 수집된 바람 데이터를 바탕으로 확률 분포도를 작성하면 어떤 크기(풍속) 또는 어떤 방향(풍향)의 바람이 얼마나 불어오는지 쉽게 파악이 가능하다1,2). 특히, 풍력 산업에서 풍속의 확률분포를 추정하는 일은 매우 중요하다. 풍력에너지는 풍속의 세제곱에 비례하므로 풍속은 풍력발전기의 발전량에 영향을 미치는 중요한 요소이다. 그러므로 특정 속도의 바람이 얼마나 불어올지를 계산해야만 풍력발전기의 정확한 발전량 추정이 가능하다. 그러므로 풍력발전기를 설치하기 전에 설치 예정 사이트에서 미리 풍속을 측정하게 되며, 이를 통계적으로 계산하여 풍속별 확률분포를 추정하게 된다.
자연풍이 갖는 풍속에 대한 확률분포는 보통 와이블(Weibull) 확률분포와 유사하므로 풍속의 도수분포함수(frequency distribution function)로 일반적으로 와이블 분포 함수가 많이 사용되고 있다. 와이블 분포는 위에서 설명한 발전량 추정 이외에도 구조물의 풍압 및 풍하중 계산 등에 사용되며, 이외에도 고장률 함수로 기계 부품의 잔존 수명 예측 및 노후화 파악 등에 사용되기도 한다. 와이블 분포는 두 개의 파라미터로 식이 구성되는데, 이는 형상계수(shape parameter)와 척도계수(scale parameter)이다. 이 두 파라미터는 와이블 분포의 형태 및 크기를 결정한다. 와이블 분포 추정 시 실제 풍속 분포에 가까운 두 파라미터가 예측되어야 하며, 부정확한 파라미터의 예측은 풍력 자원량 및 발전량, 구조물의 풍압 및 풍하중 추정 등에 있어서 오차를 발생시키는 요인이다. 그러므로 와이블 파라미터의 예측 정확도를 높일 수 있는 방안이 마련되어야 하며 이와 관련된 연구가 필요하다.
와이블 파라미터를 추정할 때 많이 사용되는 방법 중 하나가 바로 Lnleast 방법(혹은 그래프 방법(graphical method))이다. Lnleast 방법을 적용하기 위해서는 실제 풍속 데이터로부터 풍속별 누적분포함수를 계산해야 한다. 이때, 풍속 누적분포함수를 계산하기 위하여 보통 빈 방법(bin method)을 많이 사용한다3,4,5). 하지만 빈 방법 이외에도 누적분포함수를 유추할 수 있는 방법이 있으며 이는 바로 확률도시위치(PPP: probability plotting position)방법이다.
본 연구에서는 Lnleast 방법의 예측 정확도를 높이고자 경험적인 확률분포로 많이 사용되는 확률도시위치를 사용하여 풍속별 누적분포함수를 계산하였고, 이를 Lnleast 방법에 적용하였다. 본 연구의 목적은 확률도시위치를 Lnleast 방법에 적용할 때 기존의 빈 방법보다 와이블 파라미터 예측 정확도가 얼마나 향상되는지 상호 비교하는 것이다. 이를 위해 기존에 연구되었던 다양한 종류의 확률도시위치 공식을 고려하였고, 분석에 사용된 바람 데이터는 다양한 지형에서 실제 측정된 바람 데이터와 난수를 사용하여 임의적으로 추출한 가상의 바람 데이터 등 두 종류를 사용하였다. 그리고 예측 정확도 평가는 통계적인 검사 방법을 통해 수치적으로 분석하였다.
2. 와이블 분포(Weibull distribution)
와이블 분포는 확률밀도함수(PDF: probability density function), f(v)와 누적분포함수(CDF: cumulative distribution function), F(v)로 표현할 수 있으며 ,아래 식(1), (2)를 통해 계산이 가능하다3).
| $$f(v)=\frac kc\left(\frac vc\right)^{k-1}\exp\left[-\left(\frac vc\right)^k\right]$$ | (1) |
| $$f(v)=1-\exp\left[-\left(\frac vc\right)^k\right]$$ | (2) |
여기서 v는 풍속[m/s], k는 형상계수[unitless]이며, c는 척도계수[m/s]이다. 형상계수 k는 곡선의 형태를 결정하고 그 값이 감소할수록 곡선의 폭이 좁아져 뾰족한 모양으로 변하며 이로 인해 풍속변화가 적어진다. 척도계수 c는 평균풍속이 높을수록 그 값이 크다.
3. 풍속 데이터
본 연구에서 분석된 풍속 데이터는 두 종류이며, 하나는 사이트에서 실제 수집된 ‘측정 풍속 데이터’이며, 다른 하나는 통계학에서 사용하는 난수(random number)를 활용하여 인위적으로 생성한 ‘가상 풍속 데이터’이다.
3.1 측정 풍속 데이터
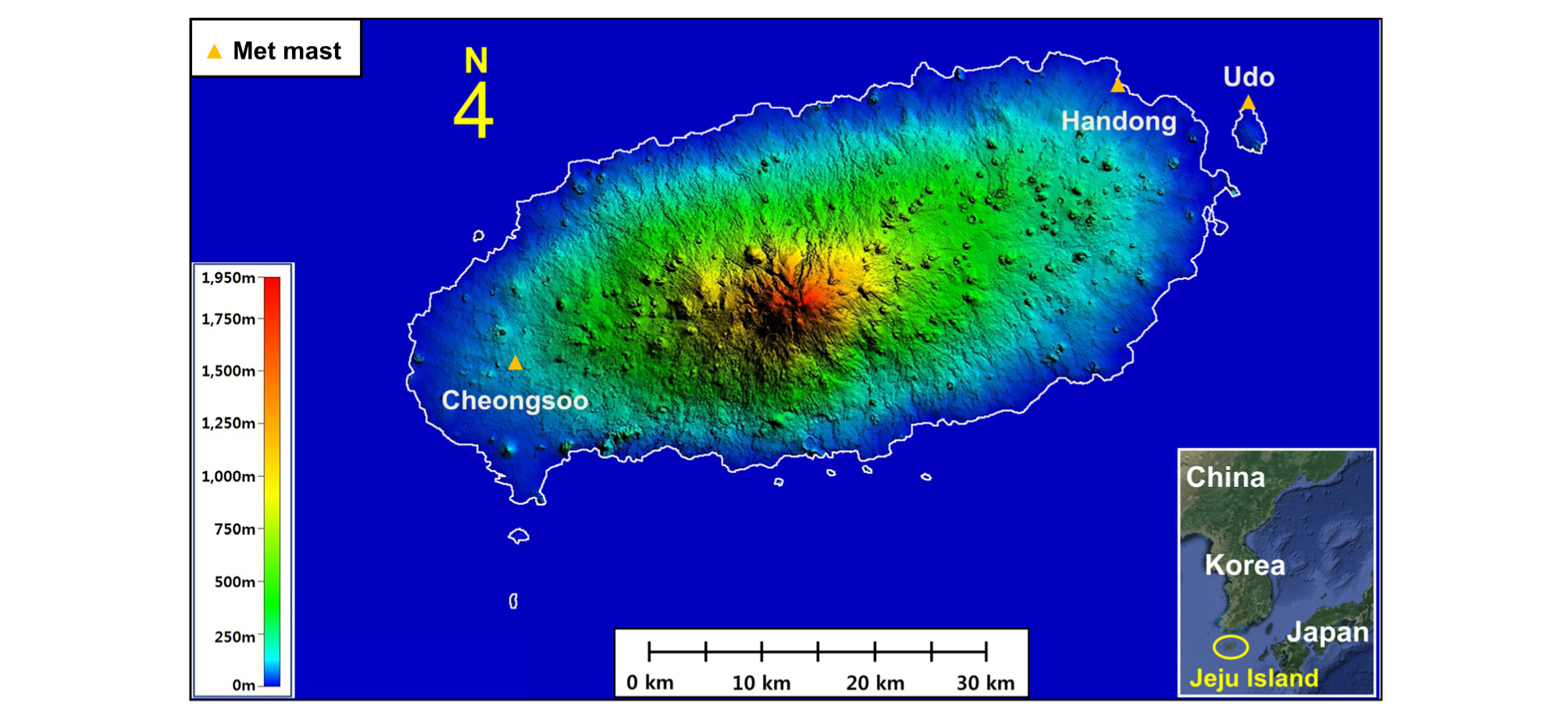
측정 풍속 데이터의 대상 사이트는 Fig. 1과 같다. 사이트는 지형에 따라 총 세 곳을 선정하였고, 섬 지형으로는 우도, 해안 지형으로는 한동, 내륙 지형으로는 청수를 선정하였다. 각 사이트에서 기상탑을 실제로 설치하여 해당 지역의 바람을 측정하였다. 자세한 사이트 정보 및 측정 현황은 Table 1과 같다. 측정 시기는 사이트 별로 상이하나 측정 기간은 모두 1년으로 동일하다. 그리고 데이터 간 동등한 비교를 위해 측정 높이는 60 m로 동일화했으며, 데이터 평균화 시간은 10분이다. 연 평균풍속은 우도 8.68 m/s, 한동 7.34 m/s, 청수 6.46 m/s 순으로 높은 값을 보였다.
Table 1. Sites and measurement conditions
해당 사이트의 지형 복잡도(terrain complexity)는 WAsP(Wind Atlas Analysis and Application Program) S/W의 지형복잡지수 RIX(Ruggedness Index) 분석 결과를 제시하였다. 그 결과 내륙 지형인 청수가 0.36%로 섬 지형인 우도 0.23%, 해안지형인 한동 0.20%보다 상대적으로 높은 지형 복잡도를 보였다. 한편, 풍속 측정에 사용된 풍속계는 세 사이트 모두 컵형 NRG #40 풍속계로 자세한 제품 사양은 Table 2와 같다.
컵형 풍속계는 상대적으로 다른 센서에 비해 높은 풍속 역치(threshold)값을 갖고 있다. 그러므로 컵형 풍속계에 의해 측정된 풍속 데이터로부터 추정된 풍속 분포는 저풍속 또는 무풍속 영역에서 실제보다 낮거나 또는 높게 왜곡될 수 있다. 그러므로 이에 대한 영향을 줄이기 위해 0.5 m/s 미만의 풍속 데이터는 분석에 사용하지 않았다. 제거된 0.5 m/s 미만의 풍속 데이터 비율은 우도는 0.57%, 한동은 1.74%, 청수는 1.17%이다.
Table 2. Anemometer specifications
| Items | Specification |
| Model | NRG #40 |
| Measuring range [m/s] | 1 ~ 96 |
| Threshold [m/s] | 0.78 |
| Accuracy | 5 ~ 25 m/s: < 0.1 m/s |
| Operational temperature [℃] | -55 ~ 60 |
| Type | 3-cup |
| Classification | Class 2.4 A Class 7.7 B |
3.2 가상 풍속 데이터
가상 풍속 데이터는 난수를 사용하여 통계적으로 추출하였다. 난수는 특정한 순서나 배열 또는 규칙을 갖지 않는 일련의 숫자들을 의미한다. 통계학적으로는 특정한 범위에서 균일한 분포(uniform distribution)를 갖는 모집단에서 추출된 표본들을 의미한다. 본 연구에서 난수는 특정한 범위(0과 1사이) 내에서 균일한 분포를 따르며, 생성된 난수들 사이에 독립성을 갖도록 임의적으로 생성하였으며, 난수 발생 방법으로는 합동법(congruential method)을 사용하였다. 참고로 합동법은 가장 널리 사용되는 난수 발생법 중 하나로 초기 값이 주어지면 재귀적 반복식에 의해서 새로운 난수를 발생시키게 된다. 난수 발생식은 식(3)과 같다6,7).
| $$X_i=(397204094\;X_{i-1})\mod(2^{31}-1)$$ | (3) |
여기서 mod는 modulus의 약자로서 앞에 제시된 숫자를 뒤에 제시된 숫자로 나눈 나눗셈의 나머지를 의미한다. 즉, a mod b는 a를 b로 나눌 때 나머지 값이다. 그리고 가상의 풍속 데이터를 얻기 위해 와이블 누적분포함수식, 식(2)를 변형한 식(4)를 사용하였다.
| $$v=c\left[\ln\left(\frac1{1-F(v)}\right)\right]^{1/k}$$ | (4) |
여기서 v는 풍속[m/s], c는 와이블 척도계수[m/s]이며, k는 형상계수[unitless]이다. 식(3)을 통해 계산된 난수를 와이블 함수의 누적분포함수로 사용하였고, 와이블 파라미터(척도계수 및 형상계수)의 경우 특정 값으로 가정하여 가상의 풍속 데이터를 생성하였다. 본 연구에서는 와이블 파라미터 값이 서로 다른 총 8가지 케이스의 가상 바람 데이터를 생성하였으며, 그에 대한 설명은 Table 3과 같다. 형상계수는 1.5, 2.0을 고려하였고, 척도계수는 2.0, 5.0, 10.0, 15.0 m/s를 고려하였다. 가상 풍속 데이터의 데이터 개수는 앞에서 설명한 측정 풍속 데이터의 수집기간인 1년을 고려하여 10분 데이터의 1년 간 데이터 개수인 52,596개(= 365.25 days/year × 24 hours/day × 6 times/hour)를 고려하였다.
Table 3. Description of the virtual wind speed data
4. 확률도시위치 공식의 Lnleast 방법 적용
4.1 Lnleast 방법(Ln-least method)
와이블 파라미터를 추정할 때 많이 사용되는 방법 중 하나는 Lnleast 방법이다. Lnleast 방법은 풍속 데이터를 로그 스케일로 보정 후 선형회귀분석을 통해 손쉽게 와이블 파라미터를 추정할 수 있다는 장점이 있으나, 다른 추정방법(모멘트 법, 최대우도법 등)에 비해 정확도가 떨어진다는 단점이 있다5,8,9).
Lnleast 방법을 활용하기 위해서는 우선 풍속 데이터로부터 선형 회귀식을 유추해야 한다. 이를 위해 와이블 누적분포함수 공식인 식(2)에 이중 자연로그함수를 취하고, 양 변을 이항하면 식 (5)와 같은 선형식을 얻을 수 있다10,11,12).
| $$\ln\;\left\{-\ln\;\left[1-F(v)\right]\;\right\}=kln(v)-kln(c)$$ | (5) |
여기서 ln(v)를 x축에 넣고 ln{-ln[1-F(v)]}를 y축에 넣어 그래프를 그리면, 선형 그래프를 얻을 수 있는데 이 때, 직선의 기울기 값이 척도계수 k가 되며, 직선의 y-절편 값 kln(c)로부터 척도계수 c를 유추할 수 있다. 식(5)를 적용하기 위해서는 풍속 누적분포함수인 F(v)를 계산하여야 한다. F(v)는 보통 빈 방법을 사용하여 각 풍속 빈에 대한 누적분포를 통계적으로 계산하여 얻게 되는데, 이때 빈 방법이란 시간열 데이터를 ‘빈(bin)’이라 불리는 특정 구간으로 나누어 분류하는 것을 의미한다. Table 4는 우도에서 측정된 바람데이터를 빈 방법을 이용하여 각 풍속 빈 별 분포 및 누적분포를 계산한 예시이며, 빈 사이즈는 1 m/s를 기준으로 하였다.
Table 4. The sample data set (site: Udo)
4.2 확률도시위치(PPP: probability plotting position) 공식의 적용
확률도시위치란 확률지에 통계치를 점으로 도시하여 얻은 경험적 확률분포를 의미하며, 이미 여러 연구를 통해 다양한 확률분포 공식이 개발된 바 있다. 본 연구의 목적은 확률도시위치 공식을 Lnleast 방법에 적용하여 기존의 빈 방법을 적용한 Lnleast 방법과 비교하여 와이블 파라미터의 예측 정확도를 높이는 것이다. 본 연구에 사용된 확률도시위치 공식은 누적 확률을 대표해야 하며, 이를 위해 기존에 연구된 총 10가지의 누적 확률도시위치 공식을 고려하였고6,13,14) 자세한 정보는 Table 5에 나타냈다. 여기서 i는 풍속 데이터를 오름차순으로 정렬했을 때 그 순위이며, n은 전체 데이터 수이다.
Table 5에서 제시된 10가지의 누적 확률도시위치 공식을 Lnleast 방법 식 (5)의 와이블 누적분포함수, F(v)에 적용하였고, 이를 통해 와이블 파라미터 k, c 값을 예측하였다. 그리고 기존의 빈 방법을 이용하여 Lnleast 방법으로 구한 k, c 값과 상호비교를 실시하여 예측 정확도를 평가하였다. 이 때, 빈 방법을 적용한 Lnleast 방법의 경우 빈 사이즈를 적게 할수록 와이블 파라미터의 예측 정확도가 높아진다는 기존 연구결과8)를 참조하여 최적의 빈 사이즈로 0.1 m/s를 선정하였다.
Table 5. Probability plotting position formulas
| No. | Name | Cumulative probability plotting position |
| 1 | Hazen | |
| 2 | California | |
| 3 | Weibull | |
| 4 | Blom | |
| 5 | Gringorten | |
| 6 | Chegodayev | |
| 7 | Cunnane | |
| 8 | Tukey | |
| 9 | Beard | |
| 10 | Median |
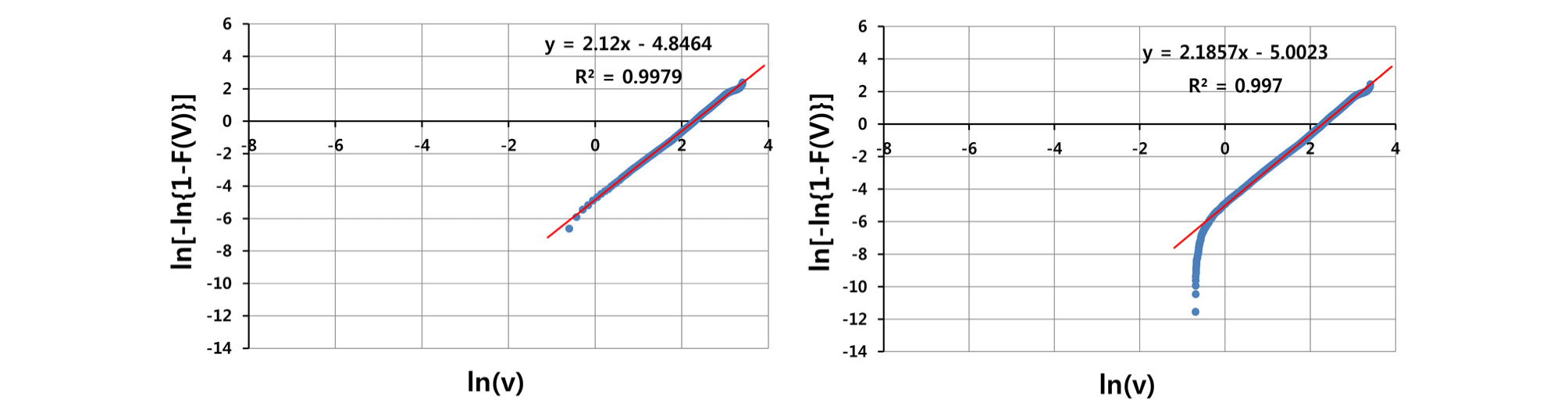
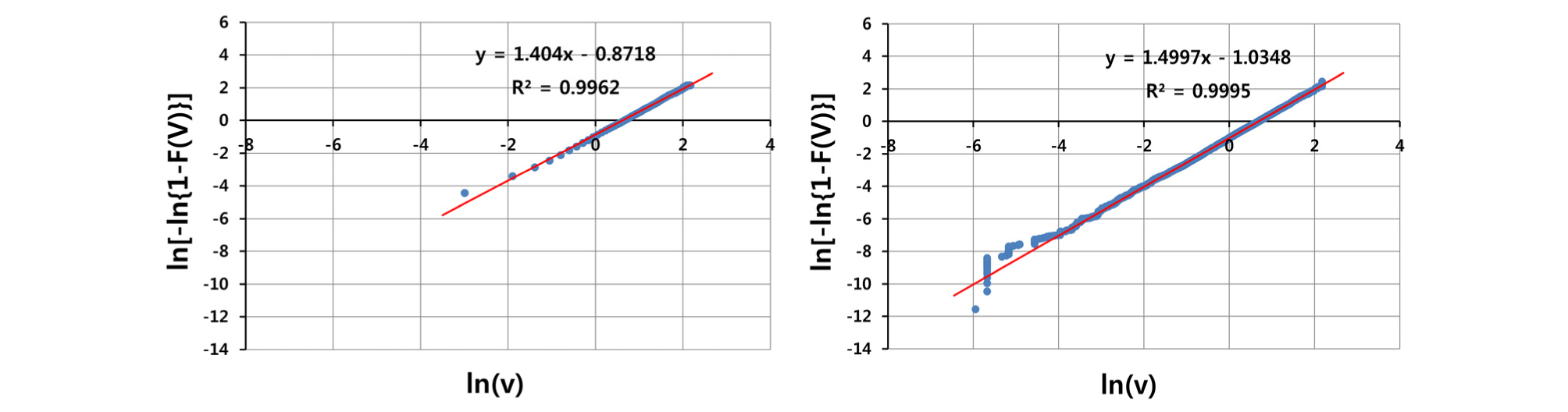
Fig. 2는 우도의 측정 풍속 데이터를 사용하여 구한 Lnleast 방법이다. 그림에서 왼쪽 그래프는 누적분포함수를 빈 방법으로 적용한 경우이며, 오른쪽 그래프는 Hazen 확률도시위치로 적용한 경우이다. 한편, Fig. 3는 가상 풍속 데이터 Case 1 (k=1.5, c=2.0 m/s)을 사용하여 구한 Lnleast 방법이다. 그래프에서 보면 저 풍속 영역에서 선형 회귀선 피팅이 잘 안 되는데 이는 자연로그 함수 ln(x)의 특성 상 x가 1보다 적은 경우 ln(x)가 급격히 감소하는 경향을 보이기 때문이다. 그러므로 1 m/s 보다 낮은 풍속에서 급격히 감소하는 ln(v)의 변화를 선형 회귀선이 피팅하기에는 한계가 있다. 이러한 차이는 빈 방법보다 Hazen 확률도시위치에서 더욱 두드러진다. 그 이유는 1 m/s 미만의 풍속 데이터 개수 차이에 있다. 빈 방법의 경우 1 m/s 미만 데이터 개수가 Hazen 법에 비해 크게 적기 때문에(Fig. 2의 경우 빈 방법은 5개, Hazen 법은 385개) 이러한 피팅 불일치가 빈 방법에서는 크게 나타나지 않는다.
5. 확률도시위치 적용 시 Lnleast 방법의 예측 정확도 비교
5.1 정확도 검사 방법
확률도시위치 및 빈 방법을 활용한 Lnleast 방법의 와이블 파라미터 예측 정확도 평가를 위해 다음 두 가지 검사 방법을 사용하였다. 첫째는 실제 값과 추정 값 사이의 오차 분석 방법으로 많이 사용되는 평균 제곱근 오차(RMSE: root mean square error)방법이며, 둘째는 추정 값이 얼마나 실제 값을 대표할 수 있는지 실제 값과 추정 값 사이의 적합성(goodness of fit)을 보여주는 결정계수(R2, coefficient of determination)이다. RMSE와 R2은 아래의 식(6)과 (7)을 사용하여 계산할 수 있다5,8,9).
| $$RMSE=\sqrt{\frac1n\sum_{i=1}^n\left[f(v_i)-\widehat f(v_i)\right]^2}$$ | (6) |
여기서 f(vi)는 실제 관측된 확률밀도 값이다. 그리고 는 Lnleast 방법에 의해서 예측된 와이블 파라미터를 식 (1)에 대입하여 구한 추정 확률밀도함수 값이다. 는 실제 관측된 확률밀도의 평균이다.
5.2 정확도 검사 결과
빈 방법 및 확률도시위치 공식을 적용한 Lnleast 방법의 정확도 비교를 위해 RMSE와 R2 검사를 수행하였다. 위 검사는 빈 방법(빈 사이즈: 0.1m/s) 및 10가지 확률도시위치 공식에 모두 적용되었다.
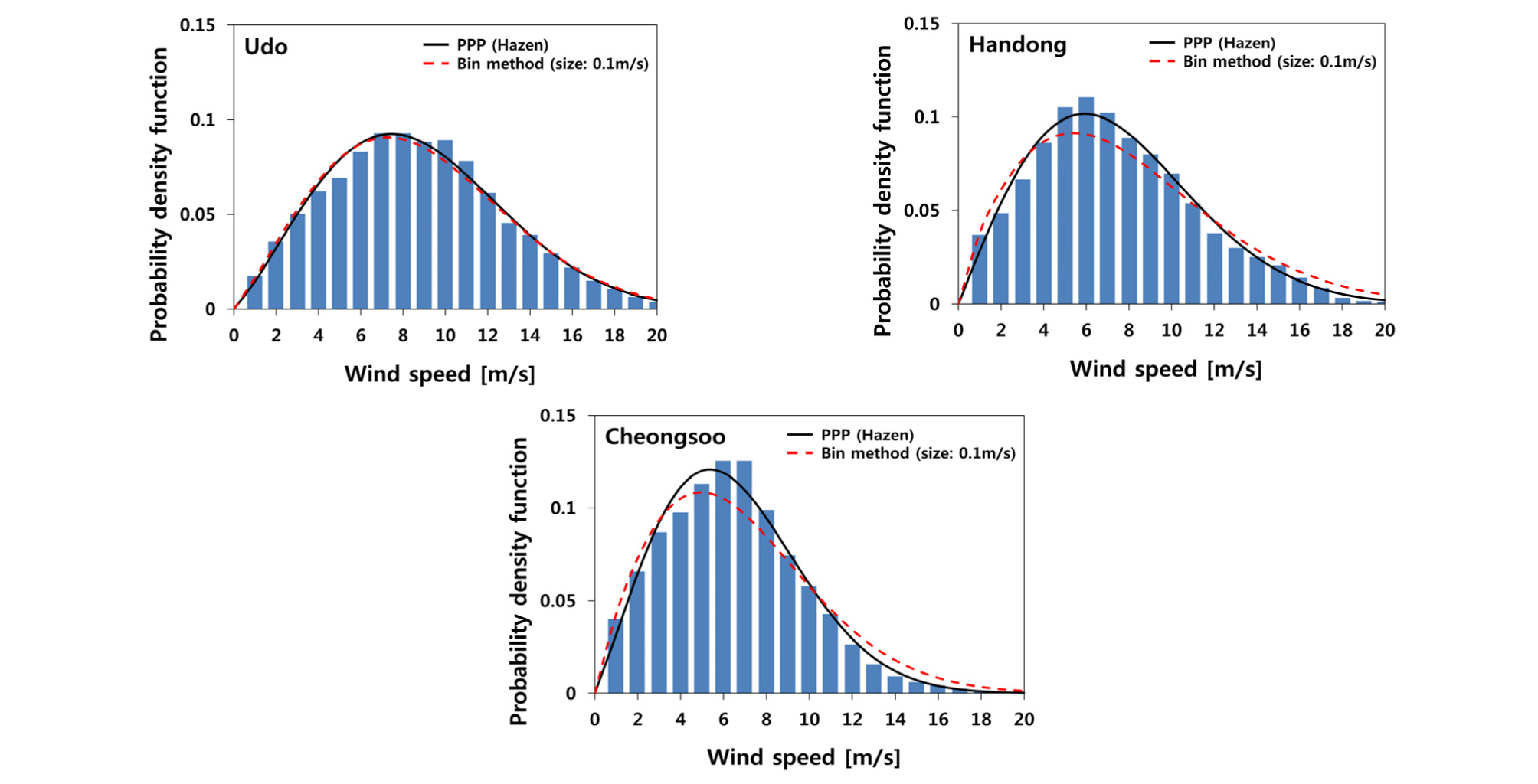
Fig. 4는 측정 풍속 데이터에서 얻은 실제 풍속 분포와 예측된 와이블 분포를 비교하는 그림이다. 세로막대가 실제 풍속 분포이며, 검은 실선과 빨간 점선은 확률도시위치와 빈 방법이 각각 적용된 Lnleast 방법으로 추정한 와이블 분포이다. 확률도시위치 공식으로는 본 연구에서 가장 정확도가 높다고 분석된 Hazen 법이 사용되었다.
Fig. 4에서 확인할 수 있듯이 모든 사이트에서 Hazen 법이 빈 방법보다 실제 풍속 분포에 더 잘 적합 된다. 그러므로 확률도시위치 적용 시 Lnleast 방법의 예측 성능이 향상됨을 확인할 수 있다. 한편, Hazen 법으로 구한 와이블 분포와 빈 방법으로 구한 와이블 분포 사이에 불일치(discrepancy)를 발견할 수 있으며, 이들 차이가 지형에 따라서 상이하였다. 특히, 섬 지형인 우도 보다는 해안지형인 한동 또는 산악지형인 청수에서 그 불일치 정도가 증가하였다. 실제로, Hazen 법 기준으로 빈 방법과 비교할 때, 정확도 향상 정도가 RMSE 검사에서는 한동(47.9%↑), 청수(40.7% ↑), 우도(16.1% ↑) 순으로 컸고, R2 검사에서도 향상 정도가 한동(1.668%↑), 청수(1.666% ↑), 우도(0.331% ↑) 순으로 컸다. 그 이유는 풍속 데이터의 변동률 차이로 보인다. 각 사이트 별 풍속 데이터의 변동 계수(coefficient of variation) 분석 결과 우도는 47.6%, 한동은 53.7%, 청수는 50.2%였다. 즉, 풍속 변동성이 큰 한동, 청수, 우도 순으로 빈 방법과 비교한 Hazen 법의 예측 정확도 향상 정도가 커지고 있다. 그 이유는 풍속 변화가 큰 바람 조건일수록 풍속 분포에 적합한 와이블 파라미터의 예측이 어렵고, 그 정도가 확률도시위치 보다 빈 방법에서 더욱 현저해지기 때문으로 판단된다.
Table 6은 측정 풍속 데이터에 적용된 Lnleast 방법의 정확도 검사 결과이다. 모든 사이트에서 확률도시위치가 빈 방법보다 높은 정확도를 보였다. 특히, 10가지 종류의 모든 확률도시위치 공식이 빈 방법에 비해 정확도가 높다는 결과가 나왔다. 그러므로 확률도시위치 적용 시 Lnleast 방법의 예측 성능이 향상됨을 확인할 수 있다.
가장 높은 정확도를 보이는 확률도시위치는 Hazen 법이며, 다음으로 Gringorten, Cunnane 법 순이었다. 하지만 확률도시위치에서 그 방법에 따른 예측 정확도 차이는 크지 않고 미미한 편이다. 확률도시위치 적용 시 Lnleast 방법의 예측 정확도 향상 정도는 Hazen 법을 기준으로 빈 방법과 비교할 때, 사이트 평균값 기준으로 RMSE 검사에서는 상대적으로 38.2% 높은 정확도를 보였으며, R2 검사에서는 1.2% 높은 정확도를 보였다.
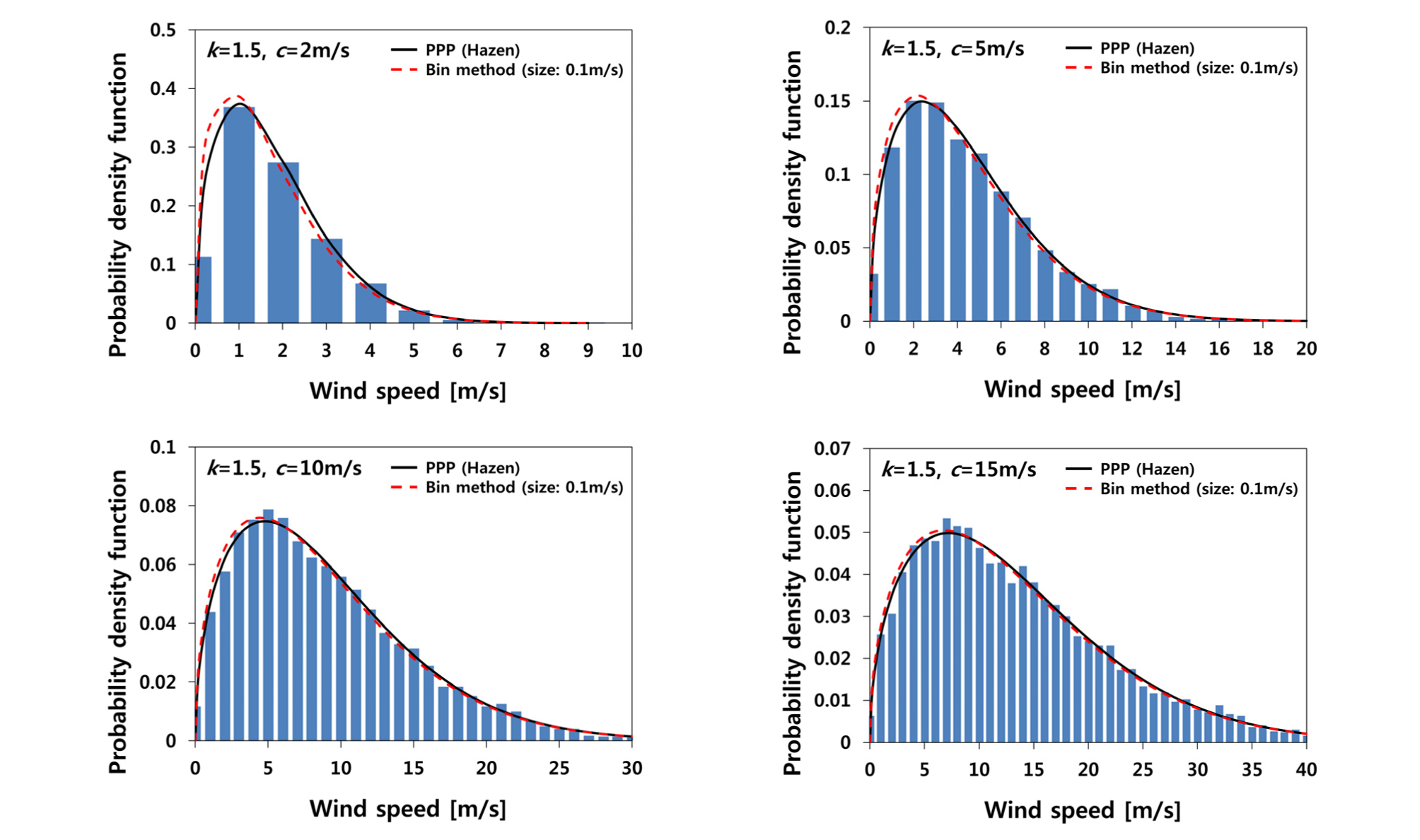
Fig. 5는 가상 풍속 데이터에서 얻은 풍속 분포와 예측된 와이블 분포를 비교하는 그림이다. Fig. 4와 비교할 때, Hazen 법과 빈 방법으로부터 예측된 와이블 분포 형태에 큰 차이는 보이지 않는다. 하지만 모든 케이스에서 Hazen 법이 빈 방법보다 실제 풍속 분포를 더 잘 적합 시킨다고 분석되었다.
Table 6. Performance results of Lnleast method for the accuracy tests (measured wind speed data)
Table 7은 가상 풍속 데이터에 적용된 Lnleast 방법의 정확도 검사 결과이다. RMSE와 R2 검사 모두 측정 풍속 데이터와 마찬가지로 모든 케이스에서 확률도시위치가 빈 방법보다 높은 정확도를 보였다. 그리고 확률도시위치 간 예측 정확도 비교 역시 측정 풍속 데이터와 마찬가지로 그 성능 차이는 크지 않았으며 정확도 순위는 Hazen, Gringorten, Cunnane 법 순이다. 가상 풍속 데이터에서 Hazen 법은 빈 방법보다 케이스 평균값 기준으로 RMSE 검사에서는 37.0%, R2 검사에서는 2.7% 높은 정확도를 보였다.
Table 7. Performance results of Lnleast method for the accuracy tests (virtual wind speed data)
빈 방법과 비교한 Hazen 법의 예측 정확도 향상 정도는 k가 일정할 때, c가 증가할수록 작아지는 경향을 보인다. 일례로 k=1.5일 때, RMSE 검사에서는 c=2.0 m/s(30.8%↑), c=5.0 m/s(28.9%↑), c=10.0 m/s(23.5%↑), c=15.0 m/s(14.4%↑) 순으로 c가 증가할수록 정확도 향상 정도가 작아진다. R2 검사 역시 c=2.0 m/s(11.8%↑), c=5.0 m/s(2.0%↑), c=10.0 m/s(0.6%↑), c=15.0 m/s(0.3%↑) 순으로 정확도 향상 정도가 작아진다. 그 이유는 가상 풍속 데이터에서 c값이 적어질수록 풍속의 분포 범위가 좁아지게 되며, 이는 빈 방법에서 활용 가능한 빈의 개수 역시 줄어드는 결과를 가져오게 된다. 빈의 개수가 줄어들면 그만큼 선형 회귀식인 식 (5)를 유추하기 위한 데이터의 수가 줄어듦을 의미하며, 이는 빈 방법의 예측 성능 저하를 가져오게 된다. 그러므로 빈 방법을 활용하여 유추된 와이블 파라미터는 그 정확도가 Hazen 법에 비해서 상대적으로 떨어질 수밖에 없다.
한편, 확률도시위치 공식은 k가 일정할 때, c가 감소할수록 예측 정확도가 작아지는 경향을 보였다. 이는 c값이 적어질수록 무풍(v=0 m/s)에 가까운 풍속의 출현 빈도가 증가하기 때문이다. 와이블 분포는 공식의 특성 상 풍속이 0 m/s일 때, f(v)가 0에서 시작한다. 그러므로 실제 분포에서 0m/s에 가까운 풍속의 출현 빈도가 높다고 한다면, 예측된 와이블 분포가 여기에 적합 되기는 매우 어렵다. 본 연구에서 사용된 가상데이터의 경우 전체 데이터 개수 기준 0.5 m/s 미만 풍속 비율은 k=1.5일 때, c=2.0 m/s(11.3%), c=5.0 m/s(3.2%) c=10.0 m/s(1.2%), c=15.0 m/s(0.6%)이다. 따라서 c값이 적을수록 실제에 가까운 와이블 분포를 추정하기 힘든 조건이며, 이에 따라서 확률도시위치 공식의 예측 정확도가 떨어지게 된다.
결론적으로 본 연구에서 가장 높은 예측 정확도를 보이는 확률도시위치 공식은 Hazen법이었다. 하지만 분석에 사용된 바람 데이터의 종류가 제한적이므로 확률도시위치공식의 정확도 순서는 바람 데이터 조건에 따라 달라질 수 있으며 이에 대한 추가 연구가 필요하다.
6. 결 론
본 연구에서는 Lnleast 방법의 예측 정확도를 높이기 위해 기존의 빈 방법을 대신하여 확률도시위치 공식을 사용하였으며, 그 성능을 상호비교 하였다. 분석에 사용된 바람 데이터는 두 종류이며, 첫째로 사이트에 실제로 설치된 기상탑에서 수집된 ‘측정 풍속 데이터’와 둘째로 난수를 활용하여 통계적으로 얻은 ‘가상 풍속 데이터’이다. 본 연구의 결과는 다음과 같다.
(1) Lnleast 방법의 와이블 파라미터 예측 정확도 비교에서 확률도시위치가 빈 방법 보다 높은 정확도를 보였다.
(2) 확률도시위치 공식에 따른 예측 정확도 차이는 미비하였으나, 전반적으로 가장 높은 예측 정확도를 보이는 공식은 Hazen 법이었다.
(3) 측정 풍속 데이터에서 빈 방법과 비교한 확률도시위치의 예측 정확도 향상 정도는 지형에 따라 상이하였고 대체적으로 지형이 복잡할수록 그 향상 정도가 컸다.
(4) 가상 풍속 데이터에서 빈 방법과 비교한 확률도시위치의 예측 정확도 향상 정도는 와이블 척도계수 값이 감소할수록 정확도 향상 정도가 커지는 경향을 보였다.
(5) 대체적으로 저 풍속 영역의 빈도가 높고, 풍속 변화가 심한 바람 조건일수록 빈 방법에 비해 확률도시위치 공식의 예측 정확도가 높았다. 그러므로 해당 사이트의 경우 와이블 풍속 분포를 추정 시 Lnleast 방법을 사용할 때 빈 방법보다는 확률도시위치 공식을 사용할 것을 추천한다.