1. 서 론
2. 실 험
3. 결과 및 고찰
3.1 타원편광법을 이용한 측정 및 모델링
3.2 Tauc Lorentz dispersion
3.3 비정질 실리콘의 타원편광분광분석
3.4 불순물 함량과의 관계 – p형 비정질 실리콘 탄화막의 타원편광분광분석
4. 결 론
1. 서 론
타원편광분광분석법(Spectroscopic Ellipsometry, SE)은 편광된 빛의 변화를 측정하는 편광광도계(polarimetry)의 일종이다. 타원편광법(ellipsometry)은 편광 상태의 빛을 시료 표면에 조사하여 반사된 빛의 편광상태 변화를 측정하는 기법으로, 이것을 분광법(spectroscopy)과 결합하여 여러 파장에 대해 측정 할 경우, 시편에 대한 여러 가지 유용한 광학적 물성을 도출할 수 있다. 특히 타원편광분광분석법은 박막 형태의 시편 및 유전체와 반도체 재료에 대해 박막의 두께 및 굴절률(refractive index, n), 흡광계수(extinction coefficient, k) 등의 정보를 도출할 수 있으며, 반도체 박막의 경우 추가적인 데이터 분석을 통해 광학적 밴드갭 (optical bandgap) 등 유용한 물성 정보를 도출할 수 있다. 특히, 반도체 및 유전체 재료의 박막증착공정이 많이 사용되는 반도체, 디스플레이 및 태양전지공정에서 타원편광분광분석법을 이용한 물성분석은 매우 중요하다. 태양전지 공정에서는 실리콘 산화막 (silicon oxide, SiO2), 실리콘 질화막(silicon nitride, SiNx) 및 산화알루미늄(Al2O3) 등 유전체 박막의 굴절률 및 박막 두께를 측정할 수 있으며, 또한 비정질 실리콘(amorphous silicon), 다결정 실리콘(polysilicon), 실리콘 탄화막(silicon carbide, SiC) 및 투명전극 금속산화막(transparent metal oxide) 등 반도체 박막의 경우 두께, 굴절률 및 소광계수와 이들 데이터를 추가적으로 가공하여 밴드갭, 공극률 및 표면거칠기 등의 정보까지 추출할 수 있다1-3).
이와 같이 타원편광분광분석법은 반도체 및 유전체 재료의 광학적 물성분석을 위해 유용하게 사용될 수 있지만, 반면 타원편광분광분석장비의 측정은 시편에 조사되어 반사된 빛의 편광상태 변화만을 탐지하는 것으로 재료의 물성과 관계된 의미 있는 정보를 얻기 위해서는 측정결과의 정밀한 모델링이 필수적이다. 그러나 측정결과의 모델링 과정은 타원편광분광분석장비의 작동원리, 편광된 빛의 성질 및 측정하고자 하는 재료의 광학적 물성 모두에 대한 이해를 바탕으로 하기에 많은 경우 대학원생 등의 사용자가 정확한 모델링을 수행하기 어려운 측면이 있다. 본 연구에서는 비정질 실리콘 및 p형 비정질 실리콘 탄화막의 타원편광분광분석 측정결과를 Tauc-Lorentz dispersion을 이용하여 모델링하고 피팅 파라미터와 비정질 실리콘 재료 물성의 상관관계에 대해 연구하였다.
2. 실 험
본 연구에서 타원편광분광분석을 위한 비정질 실리콘 재료는 플라즈마 화학기상증착법을 이용하여 제작되었다. 진성 비정질 실리콘의 경우 희석되지 않은 순수한 사일렌을 이용하여 증착하였으며 상대적으로 낮은 압력(50 mTorr) 및 낮은 RF 파워밀도(5 mW/cm2)에서 증착하였다. 또한, 비정질 실리콘 증착 시 불순물 혼입에 따른 광학적 물성변화를 관찰하기 위해 보론 도핑된 p형 비정질 실리콘 탄화막을 제작하였는데, 비정질 실리콘 증착 중 메탄(CH4) 및 디보레인(B2H6)의 유량을 같은 비율로 변화하여 시편을 제작하였다. 이와 같은 경우, 보론 도핑된 p형 비정질 실리콘의 경우 탄소(C) 및 붕소(B) 함량 증가로 인해 광학적 밴드갭 및 공극률의 변화가 발생될 것으로 예상된다.
증착된 박막은 Woollam M2000 타원편광분광분석기를 이용하여 박막의 타원편광 변화를 측정하였다. Woollam사의 M2000 타원편광분광분석기는 박막형 시편을 분석하는 데 최적화된 타원편광분광분석기로 회전보정기 및 CCD 방식 측정 및 검출 시스템을 이용하여 245 nm ~ 1240 nm의 스펙트럼 범위를 동시에 측정한다. 측정결과는 동 사의 CompleteEASE 소프트웨어를 이용하여 분석하였다.
3. 결과 및 고찰
3.1 타원편광법을 이용한 측정 및 모델링
타원편광분광분석법은 광학적 비 파괴적 분석법으로 매우 빠른 시간에 시편의 광학적 물성을 실시간으로 분석할 수 있다는 장점이 있지만, 이에 반해 단점도 존재한다. 그것은 바로 간접정보를 제공한다는 점으로 타원편광법은 일반적으로 시편에 조사되어 반사된 빛의 편광상태 변화만을 탐지하기 때문이다. 따라서 재료의 물성에 관한 정보를 직접적으로 제공하는 X선 회절분석 (XRD) 또는 라만 산란분석 (Raman scattering)과는 달리, 재료의 물성과 관계된 의미 있는 정보를 얻기 위해서는 측정결과의 정밀한 모델링이 필수적이다.
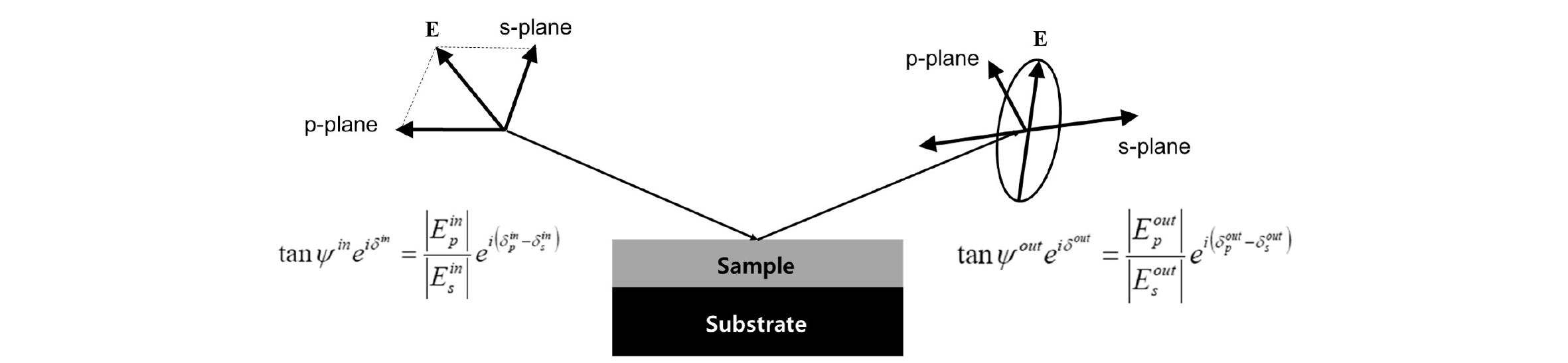
타원편광법은 기본적으로 편광된 빛을 시편 표면에 조사하고 반사된 빛의 편광상태가 어떻게 변화하였는지를 측정한다. 편광상태의 변화는 복소반사계수비, 로 정의되며 아래와 같다2).
| $$\rho={\frac{r_p}{r_s}e^{i(\triangle_p-\triangle_s)=\tan(\Psi)e^{i\triangle}}}\;$$ | (1) |
는 입사광의 편광 성분 중 p-파와 s-파 성분의 변화를 통해 정의하며, 이때 Δ는 같은 위상으로 입사한 p-파와 s-파가 반사 후 가지게 되는 상호간 위상차이며 광학적 리타던스(optical retardance) 또는 광학적 이방성 (birefringence)이라고도 부른다. 또한 tan(Ψ)의 경우 반사계수의 크기 비를 의미한다. Fig. 1은 타원편광분광분석 과정에서 입사광 및 반사광 특성의 변화를 포함한 측정과정의 모식도를 나타낸다.
상기한 바와 같이 타원편광분석을 통해 측정한 복소반사계수비는 시편에서 반사된 빛의 편광상태 변화만을 측정하며, Δ와 Ψ 만으로는 재료 물성과 관련된 의미 있는 정보를 도출하기 어렵다. 따라서 복소반사계수비를 의미 있는 물리량으로 적절히 변환하는 과정이 필요한데, 반도체 재료의 경우 가상광학상수(pseudo optical constant)라는 물리량으로 주로 나타낸다. 가상유전함수는 일반적으로 광학상수를 복소굴절률 n 및 유전함수 ε와 같이 표시하는 것과 달리 (n) 및 (ε)와 같이 표기하여 타원편광분석결과로부터 변환과정을 거친 물리량이라는 것을 표기한다2,3).
| $$<\varepsilon>=<n>^2=\sin^2(\theta_i)\cdot\left[1+\tan^2(\theta_i)\cdot\left(\frac{1-\rho}{1+\rho}\right)^2\right]$$ | (2) |
반도체 재료에 있어 유용한 광학상수는 복소굴절률(n, k) 및 복소유전함수(εr, εi)가 있는데, 이 두 광학상수는 거의 의미가 유사하지만, 각각 광자가 매질을 통과할 때 광자에 발생하는 현상(복소굴절률) 또는 재료에 빛이 입사하였을 때 재료가 반응하는 현상(복소유전함수)으로, 관점에 따라 각각 다른 과정을 표현한다. 반도체 재료에서는 특히 밴드갭 이상의 에너지를 가진 광자를 흡수하는 현상을 유전함수를 통해 해석하는 것이 적절하기 때문에 주로 유전함수 (ε)를 사용한다. 복소유전함수는 아래와 같이 정의한다2,3).
| $$\varepsilon(\lambda)=\varepsilon_1(\lambda)\pm i\varepsilon_2(\lambda)$$ | (3) |
ε1 및 ε2는 각각 복소유전함수의 실수부와 허수부를 나타내며, εr, εi 또는 εreal, εimaginary와 같이 표기할 수도 있다.
3.2 Tauc Lorentz dispersion
반도체 재료는 밴드갭 이상의 에너지를 가진 광자를 흡수하는데, 이것은 가전자대의 전자가 광자의 에너지를 흡수하여 전도대로 천이하는 현상이다. 이를 물리적으로 해석하면 원자핵과 전자 간 상호작용이며 유전분극 현상으로 설명할 수 있다. 박막 재료의 광학적 특성을 모델링하는 방법으로 Drude, Couchy 및 Sellemeier 등의 모델도 제시되어 있으나, Drude 모델의 경우 자유전자의 흡수에 의한 변화를 모델링한 것으로, 이는 금속 등 전도체의 광학적 흡수를 모델링하는데 유용한 반면,4) Couchy와 Sellemeier의 모델은 소광계수(k)가 없는 경우, 다시 말해 흡수가 없는 유전체의 경우 파장에 따른 굴절률의 변화를 모델링하는 것으로써 밴드갭이 있는 반도체를 모델링하는 데 적합하지 않다4,5).
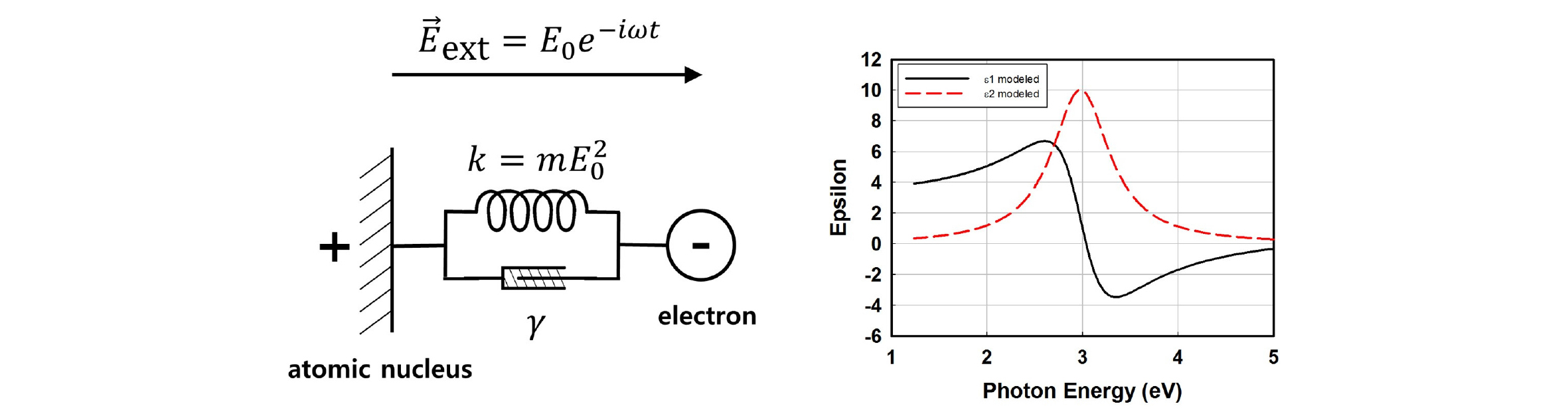
Lorentz는 반도체 재료와 광자의 상호작용을 다음과 같이 해석하였다. 무거운 원자핵 및 그 주변에 전기적 인력(쿨롱 힘, Coulomb force)으로 묶여있는 전자로 구성된 계를 고려하고, 약하게 진동하는 전기장(즉, 빛)을 가하게 되면 전자는 Fig. 2와 같이 용수철에 매달린 조그만 물체처럼 진동하게 되며, 이것을 고전적인 조화진동자 모델로 설명할 수 있다.
따라서 Lorentz oscillator는 아래와 같이 정의된다6).
| $$\widetilde\varepsilon=\frac A{{E^2}_0-E^2-irE}$$ | (4) |
여기서, γ는 damping 진동수, E0는 공명에너지(조화진동자의 고유진동수), 그리고 A는 조화진동자의 진동크기(amplitude)을 나타낸다. 특히 A는 조화진동자에서 플라즈마 공명수의 제곱(ωp2)에 해당한다. 본 모델은 기본적으로 반도체 재료와 광자의 상호작용을 표현하는 것으로써, 공명에너지 E0를 통해 직접천이 반도체의 밴드 구조를 개략적으로 나타내고 있는데, 공명에너지는 밴드구조의 임계점(critical point)에 해당하는 것으로써, 천이현상(transition)이 가장 활발히 발생하는 에너지이다. 그러나 위의 공명에너지는 가전자대(valence band), 전도대(conduction band) 및 전자의 상태밀도(density of states)를 모두 고려한 것으로써, 실제 반도체의 밴드갭과는 차이가 있다. 반도체는 밴드갭 이상의 에너지를 가진 광자부터 흡수를 시작하며, 흡수 꼬리(absorption tail)를 보이기 때문에 밴드갭은 공명에너지보다 낮은 에너지를 보이며, 일반적으로 밴드갭에너지 부근에서는 흡수 계수가 낮기 때문에, 진동자는 밴드갭에너지 부근의 에너지에서 세기가 약해진다.
이를 보완하여 반도체의 밴드갭까지 고려한 모델을 Tauc-Lorentz 모델이라고 부르며, Tauc-Lorentz 모델에서 복소 유전함수의 허수부인 εi는 소광계수 (k) 와 유사한 의미를 가지며 아래와 같이 정의된다7).
| $$\varepsilon_i=2nk=\left\{\begin{array}{l}\frac{A\cdot E_0\cdot C\cdot(E-E_G)^2}{E\cdot(E^2-E_0^2)^2+C^2\cdot E^2}\\0\end{array}\right\}\begin{array}{c}E>E_g\\E\leq E_G\end{array}$$ | (5) |
3.3 비정질 실리콘의 타원편광분광분석
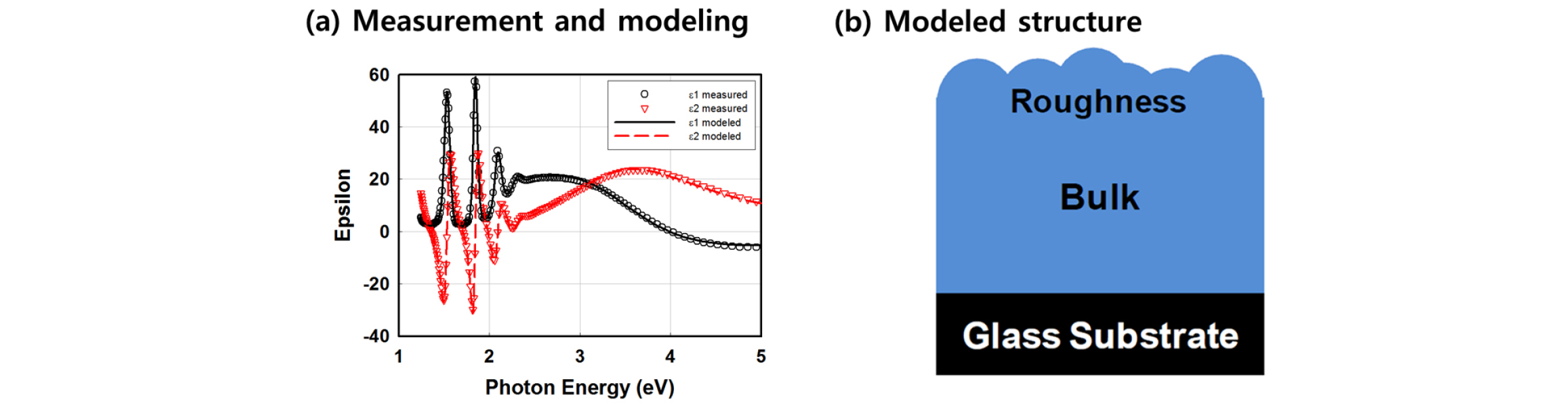
Fig. 3은 Corning XG 유리 기판 위에 증착된 진성 비정질 실리콘의 타원편광분광분석 측정 및 Tauc-Lorentz 모델링 결과이다. Table 1은 Tauc-Lorentz 모델의 피팅 파라미터 값을 나타낸다.
일반적으로 패시베이션 또는 박막 태양전지의 광 흡수층으로 사용되는 고품위 비정질 박막은 1.65 ~ 1.8 eV 범위의 광학적 밴드갭, 180 ~ 230 범위의 Amplitude, 3.5~3.7 eV 범위의 Eo 및 2.0~2.3 범위의 C 값을 보인다. 공극률이 높은 저품위 박막의 경우 C 값이 증가하고 A가 감소하게 되며, 박막의 밴드갭은 수소, 산소, 탄소 등의 불순물 함량과 관련이 있다1,7-9). Fig. 4에 Fig. 3 및 Table 1의 결과를 통해 구성한 비정질 실리콘의 유전상수를 표시하였다. 유전함수의 허수부에서 나타나는 바와 같이 Lorentz oscillator 의 저에너지 부분에 광학적 밴드갭에 의한 흡수 엣지가 표현된 것을 확인할 수 있다10).
Fitting parameters of Tauc-Lorentz model shown in Fig. 3
| Parameters | Eopt (eV) | A | Eo | C | Roughness (nm) | Thickness (nm) |
| Fitting result | 1.74 | 205 | 3.575 | 2.146 | 1.19 | 390.7 |
3.4 불순물 함량과의 관계 – p형 비정질 실리콘 탄화막의 타원편광분광분석
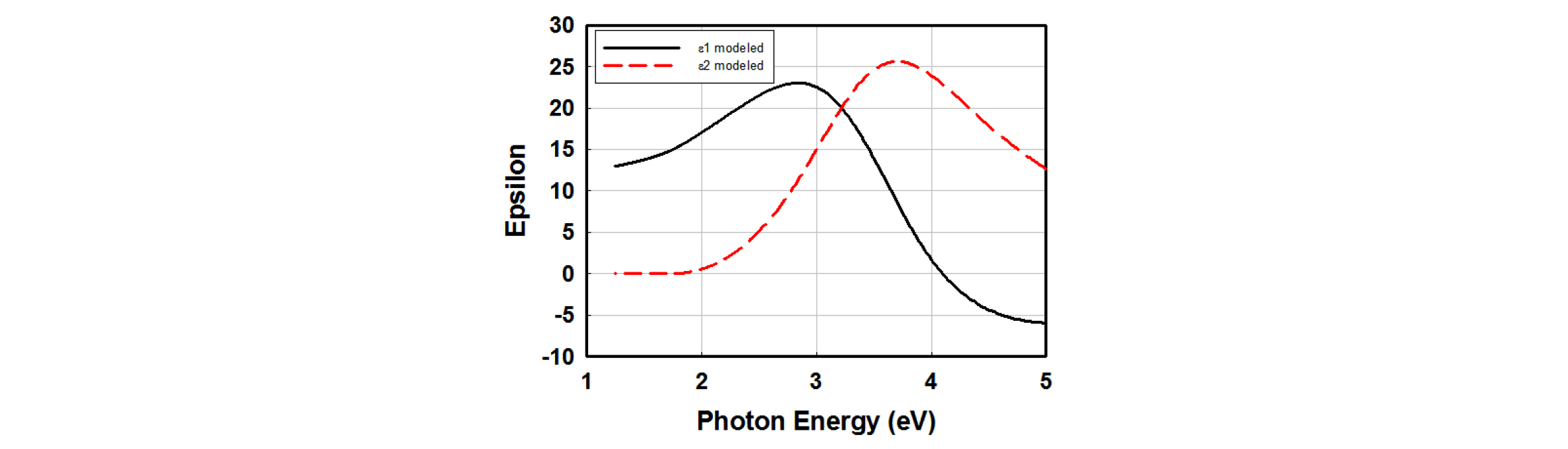
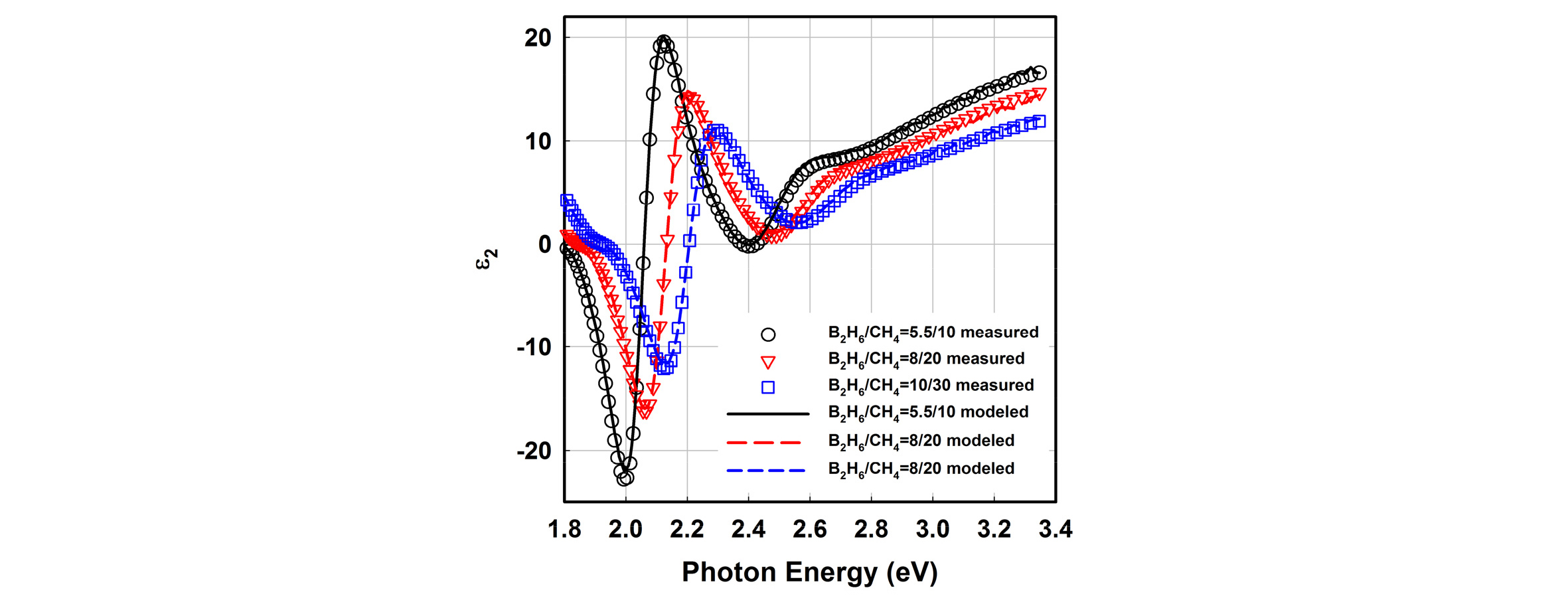
p형 도핑된 비정질 실리콘 탄화막은 비정질 실리콘에 비해 보다 넓은 밴드갭을 가지며 따라서 박막 및 결정질 실리콘 태양전지의 창 층(window layer) 재료로 사용할 경우 도핑층에 의한 기생흡수를 저감 가능하다11). 본 연구에서는 3.3절에서 연구한 비정질 실리콘의 증착 중 메탄(CH4) 및 디보렌(B2H6) 유량을 추가하여 p형 비정질 실리콘 탄화막을 증착하고 타원편광분광분석을 실시하였다. Fig. 5는 Corning XG 유리 기판 위에 증착된 p형 비정질 실리콘 탄화막의 타원편광분광분석 측정 및 Tauc-Lorentz 모델링 결과이다. Table 2는 Tauc-Lorentz 모델의 피팅 파라미터 값을 나타낸다.
Table 2 Fitting parameters of Tauc-Lorentz model shown in Fig. 5
타원편광 분석 및 모델링 결과, 박막 증착 중 메탄과 디보렌의 유량을 추가하여 박막 내 탄소 및 붕소 함량이 증가하면 광학적 밴드갭이 1.74 eV에서 1.78 eV으로 크게 증가한다. 그러나 메탄과 디보렌 유량을 각각 8/2 및 10/30 sccm으로 더욱 증가해도 박막의 광학적 밴드갭은 1.78 eV에서 1.8 eV로 추가적인 광학적 밴드갭의 변화는 현저하게 발생하지 않는다는 것을 알 수 있다. 또한, 박막 증착 중 메탄과 디보렌의 유량을 증가시키면 박막의 증착률(deposition rate)이 0.9 nm/s에서 1.5 nm/s 이상으로 변화하는 것을 확인하였다. 다만, 메탄과 보론의 유량을 증가시켰을 때 유전함수의 최고점인 A 값이 205에서 198 이하로 감소하였는데, 이것은 박막의 밀도가 낮아졌음을 의미한다. 따라서 메탄과 보론을 유량을 증가시켰을 때 관찰되는 증착률의 변화는 박막의 공극률 증가와 함께 발생하는 것으로 판단할 수 있다.
4. 결 론
본 연구에서는 Corning XG 유리 기판에 증착한 진성 비정질 실리콘 및 p형 비정질 실리콘 탄화막을 타원편광분광분석을 통해 분석하고 Tauc-Lorentz 모델을 이용하여 광학적 특성을 연구하였다. 또한 피팅 파라미터와 비정질 실리콘 재료 물성의 상관관계를 연구하였다. 타원편광분광분석은 반도체 및 유전체 재료의 광학적 물성분석을 위해 널리 사용된다. 하지만 타원편광분광분석법은 시편에 조사되어 반사된 빛의 편광상태 변화만을 탐지하는 것으로 재료의 물성과 관계된 의미 있는 정보를 얻기 위해서는 측정결과의 정밀한 모델링이 필수적이다. 향후 다양한 반도체 및 태양전지 공정에서 박막 재료의 분석에 응용 가능할 것으로 예상한다.