1. 서 론
화석연료 사용 증가로 인한 환경오염 문제 및 에너지 고갈 문제가 대두되면서 신재생에너지에 관한 관심이 크게 증가하고 있다. 이 중 태양열을 이용한 비집광형 집열기의 경우 크게 액체 가열식과 공기 가열식 집열기로 분류될 수 있다. 액체식 태양열 집열기의 경우 국내에서 가정용으로 가장 많이 보급된 집열기이나 축열조, 팽창탱크 및 배관 등의 추가 설비를 필요로 하여 별도의 설치 공간이 요구되고 열팽창, 수축 등에 의한 열매체 누설로 유지 관리에 다소 부담이 있다. 반면 공기식 태양열 집열기의 경우 추가 설비가 적게 들어 초기 투자비 및 공간적 측면에서 액체식 가열기보다 유리하며, 유지보수에 대한 부담 또한 상대적으로 적은 장점이 있다. 따라서 가열 공기를 이용 한 공간 난방, 곡류 건조 등 특정 분야에 태양열 공기 가열기가 유용하게 이용될 수 있으나, 낮은 열전도율과 열용량으로 열효율이 좋지 못하다는 단점이 있다. 따라서 국내외에서 태양열 공기 가열기 성능 향상을 위한 다수의 연구가 진행되어오고 있다.
국내의 경우 Heo et al.1)이 발열 평판을 갖는 사각 채널을 태양열 공기가열기로 모사하여 흡수판에 설치된 다양한 립(rip)및 배플(baffle) 형상에 따른 열전달 및 압력강하 특성을 전산해석을 통해 확인한 바 있다. 또한 Shin and Boo2)에 의해 태양열 공기가열기 흡열판 홀 배치 및 형상에 따른 열적 성능에 관한 수치해석 연구가 진행된 바 있으며, Kim and Boo3)는 돌출형 삼각 개구부가 설치된 태양열 공기가열기 성능에 관한 실험을 수행한 바 있다. Kim4)의 경우 흡열다공판을 이용한 태양열 공기가열기의 실험 및 수치해석 연구를 진행하였으며, Kim et al.5)은 공조시스템 적용을 위한 멀티 유로 적용 태양열 공기 가열기 운전 특성 관련 실험을 수행한 바 있다. 또한 Choi et al.6,7)은 태양열 공기가열기 공기 채널 내 핀(fin) 형상에 따른 전열성능에 관한 연구를 진행한 바 있으며, 이중 하나의 핀이 적용된 태양열 공기-물 가열기에서의 공기 가열 성능에 관한 실험을 수행한 바 있다.
국외의 경우 Karim and Hawlader8,9)에 의해 V-groove형상을 갖는 흡수판과 및 핀이 부착된 흡수판이 이용된 태양열 공기 가열기에 대한 실험 및 수치해석이 진행된 바 있다. Yadav and Bhagoria10-12)의 경우 전산해석을 통해 흡수판에 수평형 삼각형, 사각형, 원형 형상의 저항체가 설치된 태양열 공기가열기의 열적 성능에 대한 연구를 수행한 바 있다. 또한 Singh et al.13)은 전산해석을 통해 흡수판에 여러 형상의 립(rip) 구조물이 부착된 태양열 공기가열기의 열적 성능을 분석하였다. Ebru and Faith14)의 경우 흡수판에 부착된 핀(fin) 형상에 따른 태양열 공기 가열기 성능을 실험적으로 분석하였고, Singh15)의 경우 태양열 공기 가열기 공기 채널 형상 변경을 통한 성능 향상 관련 전산해석 연구를 진행하였다. 또한 Singh et al.16)과 Saini and Maithani17)는 각각 갭(gap)을 갖는 V-립(rip)과 원호(Arc) 형상의 립(rip)이 설치된 흡수판에서 립(rip) 형상 조건에 따른 공기채널 내 유동 공기로의 열전달 성능 및 마찰인자에 관한 상관식을 제시하였다. 이 외에도 다수의 연구가 진행된 바 있으나, 주로 흡수판의 변형 혹은 구조물 부착에 따른 연구가 주를 이루고 있다18,19).
하지만 태양열 공기-물 가열기 혹은 공기식 태양광/열 모듈과 같이 흡수판 변형이 용이하지 않은 시스템의 경우 공기가열성능 향상을 위한 흡수판 변형 및 구조물 부착을 통한 제작 등에 어려움이 있다. 따라서 비교적 제작이 용이하고 흡수판 변형이 어려운 태양열 집열기에 적용될 수 있는 저항체들의 형상에 따른 전열성능에 관한 연구가 진행된 바 있으며, 이 중 수평형 사각저항체가 다른 형상보다 좀 더 우수한 것으로 판단되었다20). 다만 이러한 수평형 사각저항체의 경우 높이 및 길이, 설치 간격 등의 설치 조건에 따라 그 성능이 변하게 된다. 따라서 본 연구에서는 태양열 공기가열기 공기 채널 내 수평형 사각저항체 설치 조건에 따른 열전달 및 압력강하 성능을 전산해석에 근거해 평가해보고 향후 실제 적용 가능성 등을 확인해보고자 하였다.
2. 수치해석 모델 및 방법
2.1 수치해석 모델
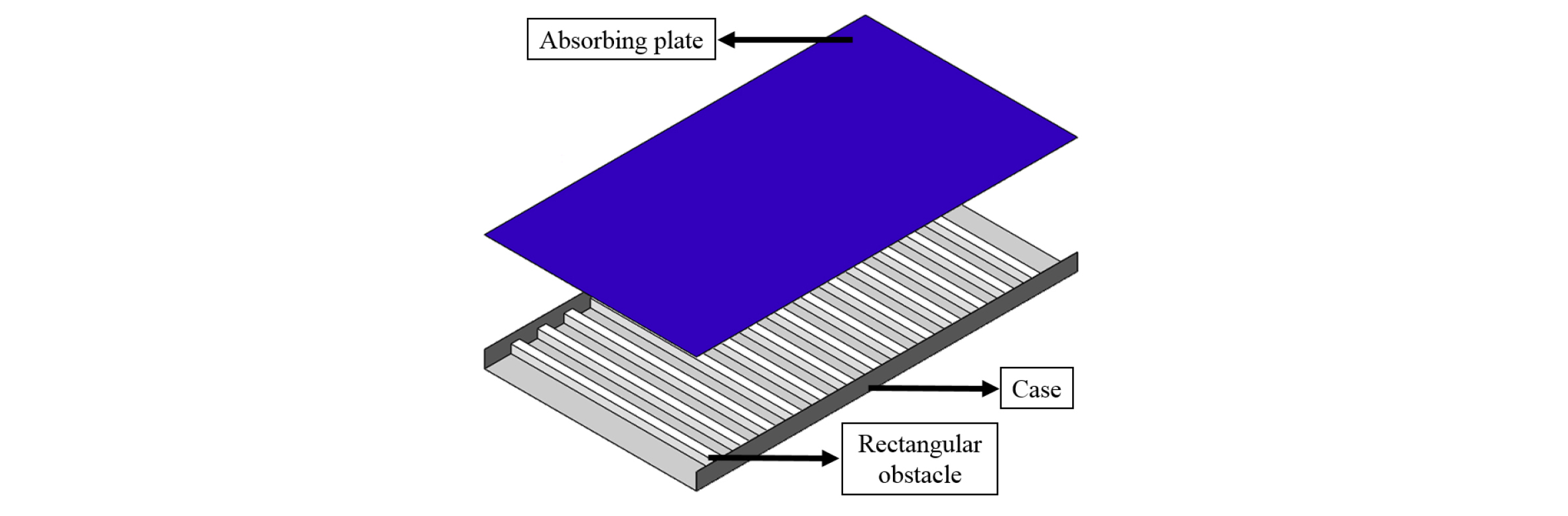
본 연구에서는 Fig. 1에 나타난바와 같이 사각저항체가 설치된 태양열 공기가열기에서 해당 저항체 설치 조건에 따른 열전달 및 압력강하 성능을 평가해보고자 하였으며, 태양열 공기가열기 내에서의 공기 유동이 유동 방향 기준 대칭이므로 해석의 간편화를 위해 관련 논문들의 연구를 참고하여10-12) 2D 모델을 이용한 분석을 수행하였다.
제작된 모델의 전열부는 길이 1800 mm, 너비 500 mm, 높이 80 mm로 되어있으며 전열부 입‧출구에서의 완전 발달 유동을 위해 ASHRAE Standard 9321)의 기준을 참고하여 입구 측 400 mm, 출구 측 700 mm의 덕트를 구성하였다. 또한 전열부 윗면에는 1000 W/m2의 일정 열유속 조건이 주어졌으며, 유입 공기 온도 26.85℃(300K), 출구 조건 대기압, 그 외 공기채널 외면은 단열 조건을 부여하였다. Fig. 2에는 해석에 수행 모델의 개략적 모습과 경계 조건을 나타내었다.
2.2 수치해석 방법
본 연구에서는 태양열 공기가열기 내 사각저항체 설치 조건에 따른 전열성능을 평가하기 위해 상용 열유체 프로그램 중 하나인 ANSYS Fluent 17.222)을 이용하였다.
각 사각저항체 설치 조건은 덕트 높이 대비 저항체 높이(e/h) 값 0.2, 0.5, 0.8, 사각저항체 높이 대비 저항체 길이(l/e) 값 0.5, 1.0, 1.5, 사각저항체 설치 간격에 대한 전열부 길이(L/p) 값 8, 12, 18로 주었다. 해석은 각 높이 조건에서, 길이 및 설치 간격을 변화시키며 총 27개의 설치조건에 대해 수행하였으며, Fig. 3과 Table 1에 사각저항체 형상 조건과 해석 조건을 각각 나타내었다.
Table 1 Simulation conditions
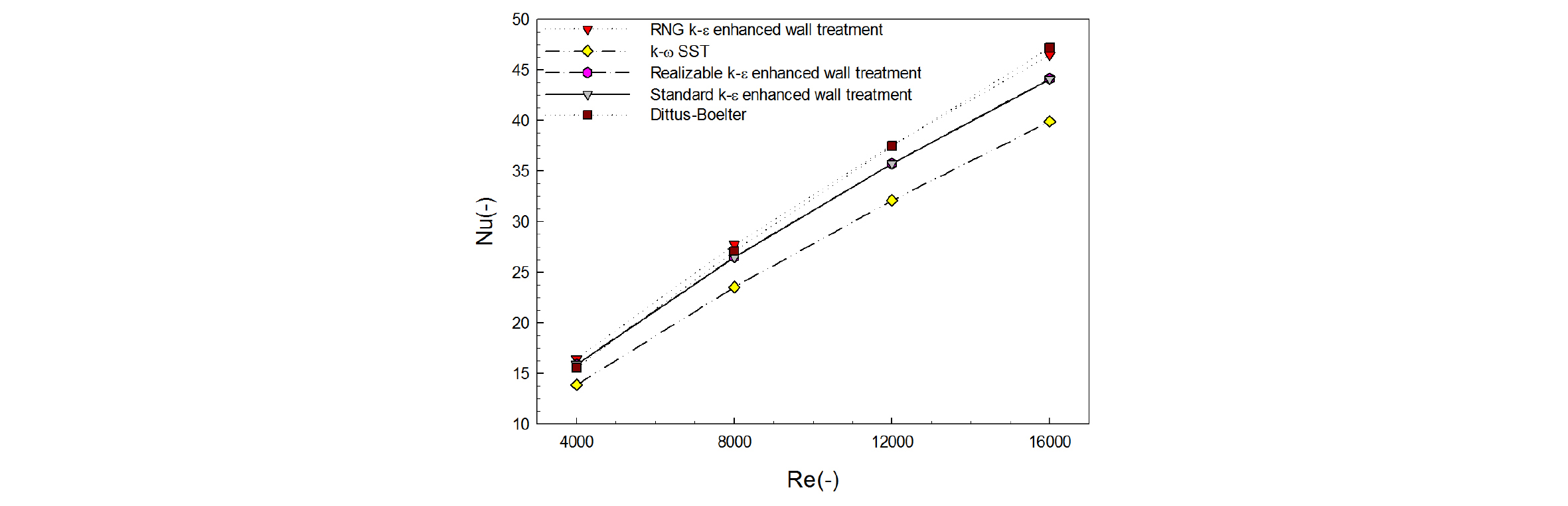
해석은 종래 연구들이 태양열 공기가열기 운전 조건을 고려하여 Reynolds 수 4,000에서 20,000의 범위에 대해 주로 조사한 것을 참고하여 해당 Reynolds 수의 중간 값인 12,000로 수행하였고,10-13) 수력직경 0.13793 m 고려 시 풍속은 1.2708 m/s이다. 또한 해당 조건은 난류 영역에 해당하므로 해석의 타당성 검증을 위해 사각저항체가 설치되지 않은 공기 채널에서 여러 난류 모델을 사용하여 얻어진 결과 값과 매끈한 덕트에서의 열전달 성능을 나타내는 Dittus-Boelter 실험식을 비교하였다23). 그 결과 Fig. 4에 나타난바와 같이 대체로 실험식과 유사한 값을 보였으나, 이 중 RNG k-ɛ 모델24)이 절대 평균 퍼센트 오차 2.47%로 가장 오차가 적어 해당 난류 모델을 해석에 이용하였고 결과 값의 수렴조건은 연속방정식 10-4, 에너지방정식 10-6미만으로 정하였다.
3. 결과 및 고찰
3.1 열전달 성능
해당 연구에서의 공기 채널 외면은 단열 조건으로 사각 저항체 형상이 바뀌어도 열전달량은 발열 조건인 1000 W/m2으로 동일하게 된다. 따라서 본 연구에서는 태양열 공기가열기 내 사각저항체 설치 조건에 따른 열전달 성능 비교를 위해 Nu수를 확인하였으며, 이는 해석 결과에서 얻어진 값과 다음과 같은 식으로부터 구해질 수 있다.
| $$Nu=\frac{h_{air}D_h}{k_f}$$ | (1) |
이때 대류 열전달계수와 공기 평균온도는 다음과 같다.
| $$h_{air}=\frac{{\dot Q}_{air}}{A_s(T_s-T_{air,avg})}$$ | (2) |
| $$T_{air,avg\;}=\frac{T_{air,out}-T_{air,\;in}}2$$ | (3) |
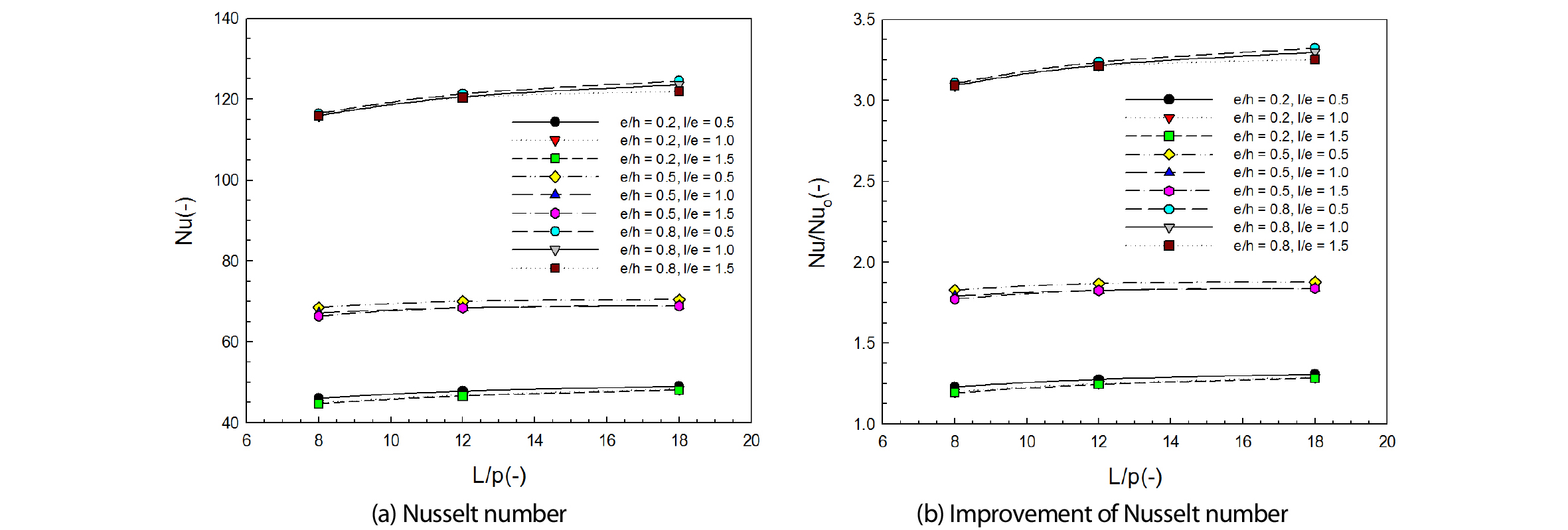
Fig. 5에는 사각저항체 설치 조건에 따른 열전달 성능을 나타내었다. 사각저항체 설치 조건에 따라 Nu수는 46.57에서 124.53의 값을 보였고, 최소 1.2배에서 최대 3.32배까지 열전달 성능이 향상되는 것을 확인할 수 있었다.
사각저항체 설치 조건에 따른 열전달 성능의 경우 설치 높이가 높아질수록 열전달 성능이 향상되는 모습을 보였으며, 이는 저항체 높이가 높을수록 공기 유동면적이 작아져 사각저항체와 열전달이 발생하는 전열부 사이의 공기 유동 속도가 증가하였기 때문으로 사료되었다. 또한 사각저항체 길이 및 설치 간격 변화에 따른 열전달 성능의 경우, 길이가 작을수록, 설치 간격이 조밀할수록 열전달 성능이 증가하는 모습을 보였다. 이는 길이가 작을 시 국부적인 속도 증가영역에서 저항체에 의한 마찰을 덜 받기 때문으로 사료되었으며, 설치 간격이 조밀할 경우 사각저항체 설치 개수가 늘어나면서 속도 증가 구간이 많아졌기 때문으로 판단되었다.
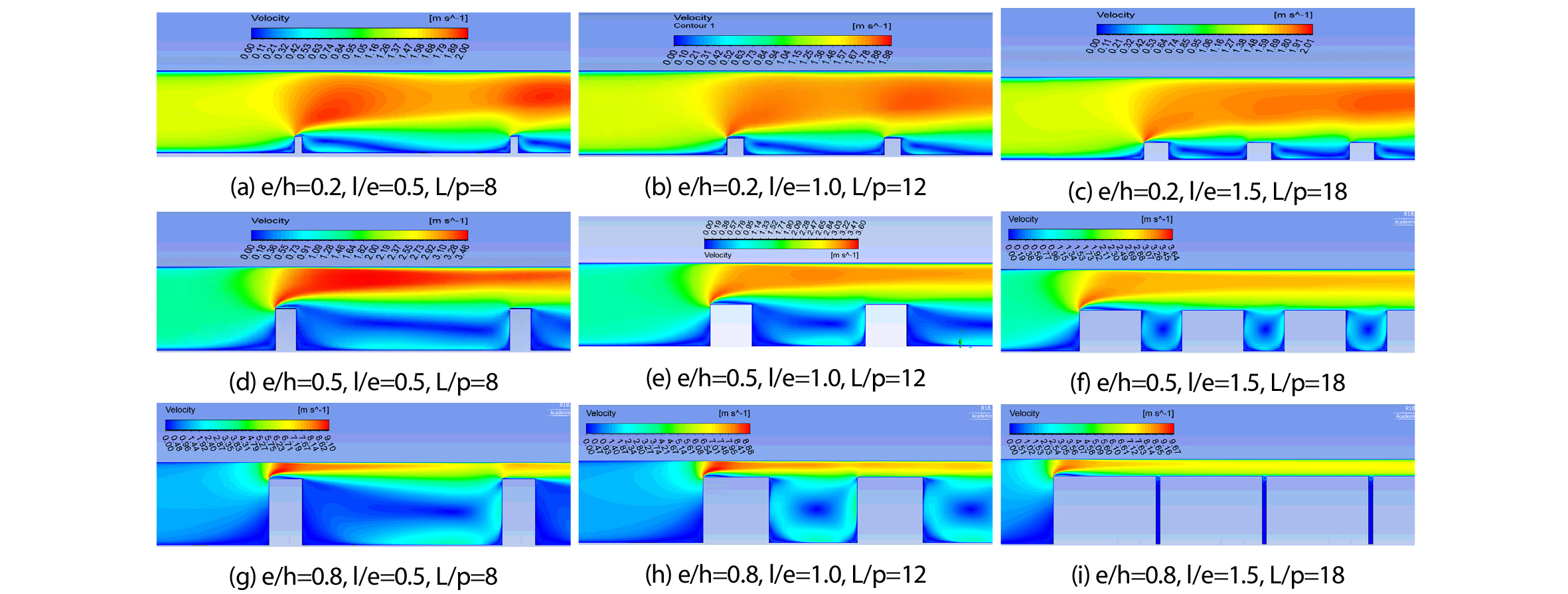
이때, 형상 조건 중간 값인 e/h=0.5, l/e=1.0, L/p=12을 기준으로 각 형상 조건 변화에 따른 열전달 성능 변화를 확인해보면 높이만의 변화로 최대 76.4%정도의 열전달 성능 향상이 이뤄졌으나, 길이 및 설치 개수 변화로 인한 열전달 성능은 각각 최대 2.4%, 1.9%정도의 향상을 보였다. 이로부터 열전달 성능 향상에 높이의 영향이 가장 크며 길이 및 설치 간격의 변화에 따른 영향은 다소 미미한 것으로 판단되었다. Fig. 6에는 사각저항체 설치 조건에 따른 유동장에서의 속도등고선을 나타내었다.
3.2 압력강하
앞서 확인한대로 사각저항체 설치 시 유동 공기의 국부적인 속도 증가에 따른 열전달 성능 향상이 가능하나, 사각저항체가 유동에 저항으로 작용하며 압력강하 값이 커지게 된다. 따라서 해당 연구에서는 해석 결과와 아래와 같은 Modified Blasius 식을 통해 구한 마찰인자 값 비교를 통해 압력강하 증가 정도를 확인하였다25).
| $$f=\frac{(\triangle P/L)D_h}{2\rho v^2}$$ | (4) |
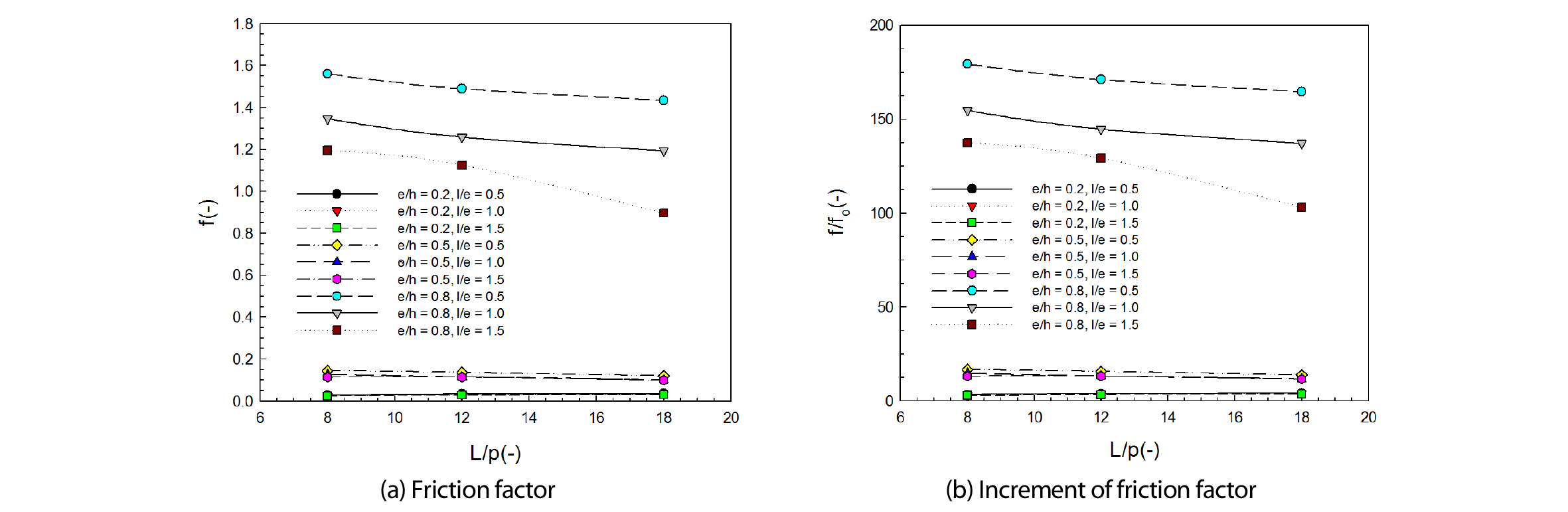
Fig. 7에는 해석 결과 값과 식(4)로부터 얻은 마찰인자를 나타내었으며, 설치 조건에 따라 0.024에서 1.561까지 다양한 값을 보였고 사각저항체가 설치되지 않은 경우 대비 최소 2.8배에서 최대 180배까지 마찰인자 값이 증가하였다.
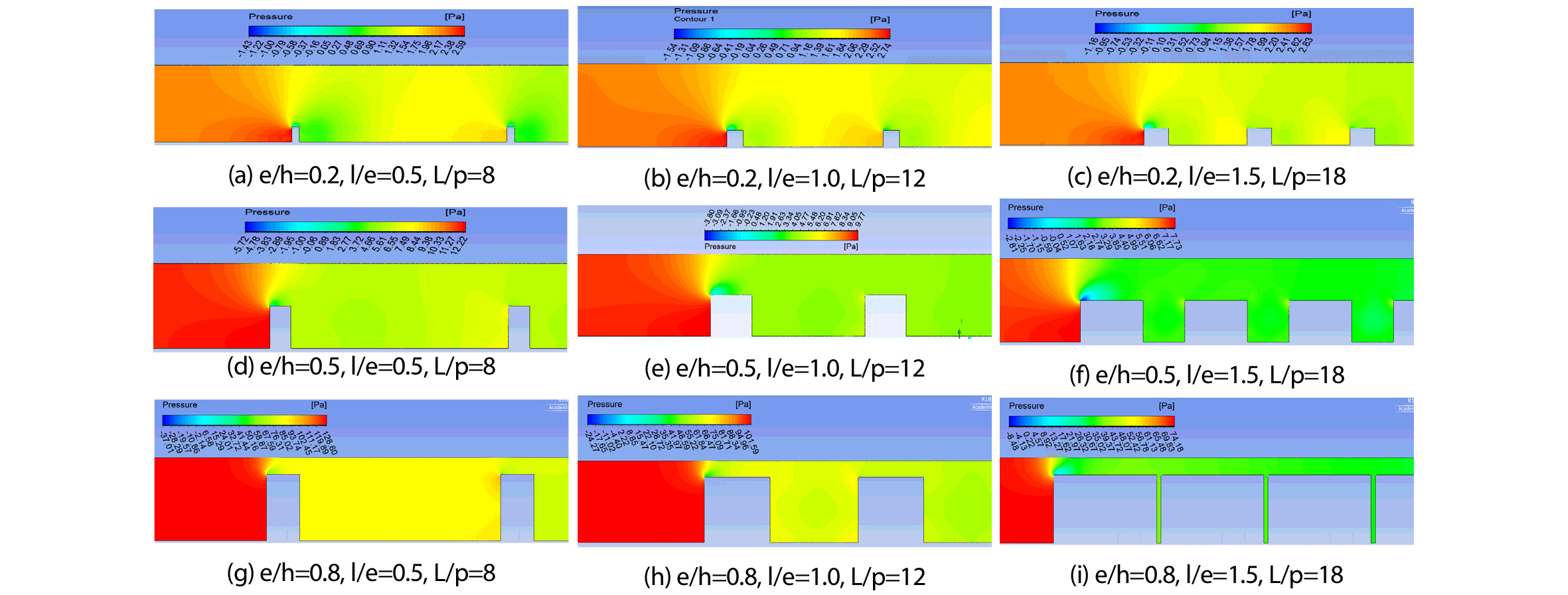
사각저항체 형상 조건 변화에 따른 마찰인자의 경우 설치 높이가 증가할수록 유동 공기에 저항으로 작용하는 부분이 많아져 그 값이 커지는 모습을 보였고, 길이 변화에 따른 압력강하의 경우 모든 높이 조건에서 사각 저항체 길이가 길수록 와류 영역이 감소하여 압력강하 값이 적어지는 것을 알 수 있었다. 설치 간격에 따른 마찰인자의 경우 높이 조건 e/h=0.2에서는 설치 간격이 조밀해지면서 주유동에 방해로 작용하는 사각 저항체 설치 개수가 많아져 마찰인자 값이 증가하는 모습을 보였다. 하지만 높이 조건(e/h) 0.5 및 0.8에서는 설치 간격이 조밀해지면서 압력강하 값이 적어지는 모습을 보였으며, 이는 높이가 높은 조건에서의 사각저항체 길이가 높이 조건(e/h) 0.2보다 더 크기 때문에 설치 간격이 조밀해질수록 사각 저항체 후단부에서의 와류영역이 감소하고 사각 저항체 상부로 주유동이 형성되면서 유동 공기의 확대 및 축소가 적어졌기 때문으로 판단되었다26).
또한 앞서 확인한바와 같이 사각저항체 높이가 높을수록, 길이가 적을수록 열전달 성능이 향상되나 마찰인자 값도 증가하는 모습을 보여 사각저항체 높이 및 길이 변화로 인한 열전달 성능 향상에 압력강하 증가가 수반되는 것을 확인할 수 있었다.
Table 2 및 Fig. 8에는 사각저항체 형상조건에 따른 압력강하 등고선과 압력강하의 정량적 결과 값을 각각 나타내었으며, 앞서 확인한 바와 같이 높이가 높을수록 압력강하가 크게 일어나고, 높이 e/h=0.2에서는 길이가 길고 설치 간격이 조밀할수록, 높이 e/h=0.5 및 e/h=0.8에서는 길이가 짦고 설치 간격이 넓을수록 압력강하 정도가 커지는 모습 보였다.
Table 2 Pressure drop with respect to installation conditions of rectangular obstacle
3.3 성능계수
앞서 사각저항체 설치 조건 변화에 따른 열전달 성능과 마찰인자에서 확인한 바와 같이 사각저항체 설치 조건 변화에 따른 열전달 성능 향상에 압력강하 증가가 수반되는 것을 알 수 있었다. 따라서 사각저항체 설치에 따른 열전달 성능 향상과 압력강하 증가 모두 고려할 필요가 있으며, 이를 위해 본 연구에서는 Webb과 Gee에 의해 제시된 압력강하 증가 대비 열전달 성능 향상 정도를 나타내는 성능계수를 이용하였다27).
| $$PF=\frac{Nu/Nu_o}{(f/f_o)^{1/3}}$$ | (5) |
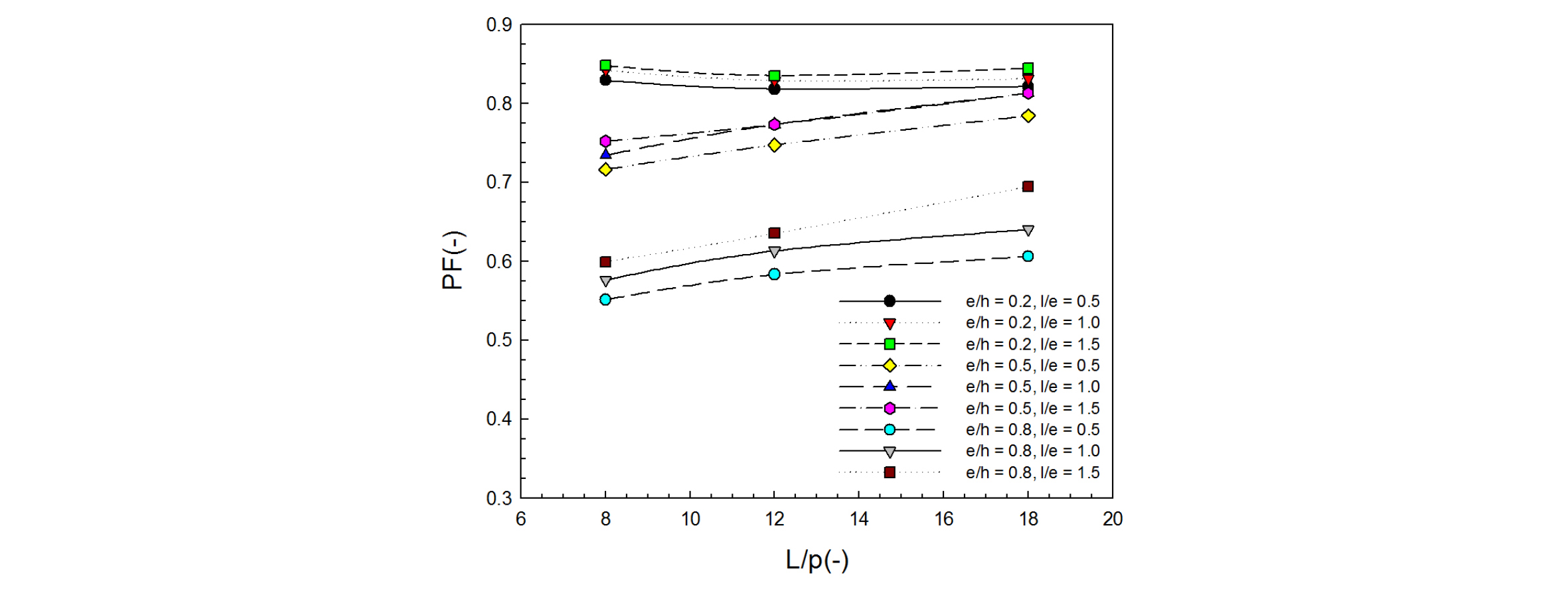
이때, 와 는 사각저항체가 설치되지 않은 경우의 Nu수와 마찰인자 값이다. Fig. 9에는 사각저항체 설치 조건에 따른 성능계수를 나타냈으며, 사각저항체 설치 조건에 따라 최소 0.538에서 최대 0.828의 값을 보였다.
사각저항체 설치 조건에 따른 성능계수의 경우 높이 증가에 따라 성능계수 값이 감소하는 모습을 보였다. 즉, 사각저항체 높이 증가에 따른 열전달 성능 향상에 이보다 더 큰 압력강하가 수반됨을 알 수 있었다. 길이 변화에 따른 성능계수의 경우도 길이가 작을수록 성능계수 값이 감소하는 모습을 보여, 동일 높이 및 설치 간격에서 사각저항체 길이 감소에 따른 열전달 성능 향상보다 압력강하가 더 크게 일어남을 알 수 있었다.
설치 간격 변화에 따른 성능계수의 경우 높이 조건(e/h) 0.2에서는 설치 간격이 넓은 L/p=8의 조건에서 가장 높은 성능계수 값을 나타내었으나 높이 조건(e/h) 0.5 및 0.8의 조건에서는 설치 간격이 작을수록 성능계수 값이 커지는 모습을 보였다. 이는 앞서 확인한바와 마찬가지로, 높이 조건(e/h) 0.5 및 0.8에서 설치 간격이 조밀할수록 열전달 성능은 향상하고 압력강하 정도는 감소하였기 때문으로 사료되었다.
위와 같은 결과로부터, 열전달 성능 향상 측면에서는 사각저항체 높이가 높을수록, 길이가 적을수록, 설치 간격이 조밀할수록 유리한 모습을 보이나, 압력강하를 고려한 성능계수의 경우 높이 조건(e/h) 0.2에서는 높이가 낮을수록, 길이가 길수록, 설치 간격이 넓을수록 더 높은 성능계수 값을 보이며 높이 조건(e/h) 0.5 및 0.8에서는 높이가 낮을수록, 길이가 길수록, 설치 간격이 조밀할수록 성능계수 값이 큰 것을 알 수 있었다.
또한 열전달 성능 향상과 압력강하를 고려한 성능계수의 경우 높이 조건(e/h) 0.2, 길이 조건(l/e) 1.5, 설치 간격(L/p) 8에서 가장 큰 값을 보였으나 열전달 성능 향상 자체는 가장 적은 것을 알 수 있었다. 이는 사각저항체 설치 조건 변경에 따른 열전달 성능 향상에 대체로 더 큰 압력강하 증가가 수반되기 때문으로 판단되었으며, 향후 실제 태양열 공기가열기 적용 적합 설치 조건 선정을 위해서는 필요 열전달 성능 향상 정도와 허용 압력강하에 대한 추가적인 고려가 수반되어야 할 것으로 사료되었다.
4. 결 론
본 연구에서는 흡열판 변형 및 구조물 부착 등이 어려운 시스템에 적용될 수 있는 수평형 사각저항체가 태양열 공기가열기에 설치되었을 때 설치 조건에 따른 열전달 성능과 압력강하를 확인해보았으며 다음과 같은 결론을 얻을 수 있었다.
(1) 사각저항체 설치 조건에 따른 열전달 성능의 경우 설치 조건에 따라 최소 1.2배에서 최대 3.32배까지 향상되는 모습을 보여 유효한 열전달 성능 향상이 가능함을 확인할 수 있었다. 또한 설치 조건에 따라 설치 높이가 높을수록, 길이가 적을수록, 설치 간격이 조밀할수록 열전달 성능이 향상되는 것을 알 수 있었다.
(2) 마찰인자의 경우 사각저항체 설치로 인해 최소 2.8배에서 최대 180배까지 그 값이 증가하였으며, 높이가 높을수록 마찰인자 값이 커지는 경향을 보였다. 길이 및 설치 간격에 따른 마찰인자의 경우 높이 조건 e/h=0.2에서는 저항체 길이가 길수록, 설치 간격이 조밀할수록 마찰인자 값이 커졌으며 높이 조건 e/h=0.5 및 0.8인 경우 길이가 적을수록, 설치 간격이 넓을수록 와류 영역 증가로 마찰인자 값이 커지는 모습을 보였다.
(3) 태양열 공기가열기 내 사각저항체 설치로 인한 열전달 성능 향상과 압력강하 증가를 같이 고려하기 위해 성능계수를 확인해본 설치 조건에 따라 최소 0.538에서 최대 0.828의 값을 보였으며 높이가 낮을수록, 길이가 길수록 성능계수 값이 커지는 모습을 보였다. 또한 설치 간격에 따라 높이 조건(e/h) 0.2인 경우 설치 간격이 넓은 조건에서 성능계수가 큰 값을 보였고, 높이 조건(e/h) 0.5 및 0.8에서는 설치 간격이 조밀할수록 성능계수가 증가하는 모습을 나타내었다.
(4) 위와 같은 결과로부터 사각저항체 설치로 인한 열전달 성능 향상에 그보다 더 큰 압력강하가 수반됨을 알 수 있었다. 따라서 본 연구의 결과를 토대로 향후 해당 저항체가 적용된 태양열 공기가열기에서의 온도 상승, 열효율, 송풍 동력 등의 확인을 통해 필요 열전달 성능 향상 정도 및 허용 압력강하에 대한 추가적인 고찰이 필요할 것으로 판단되었다.
기호설명
h: Convective heat transfer coefficient [W/m2K]
: Heat transfer rate [W]
T: Temperature [℃]
Ts: Temperature of heat plate [℃
As: Heat transfer area [m2]
kf: Thermal conductivity [W/mK]
: Pressure drop [Pa]
Dh: Hydraulic diameter [m]
v: Velocity [m/s]
Nu: Nusselt number [-]
Re: Reynold’s number [-]
f: Friction factor [-]
PF: Performance factor [-]