1. 서 론
2. 해석방법
2.1 시스템 모델 및 수치해석
2.2 CTSF 를 구하는 수치해석 과정의 일반화
2.3 CTSF 계산용 입력데이타
3. 결과 및 고찰
3.1 복합지붕 R18
3.2 복합벽체 W19
4. 결 론
1. 서 론
냉방부하를 구하기 위해 제안된 방법 중 하나는 복사시계열 방법(Radiant Time Series Method(RTS))이다.1,2)복사시계열 방법 (RTS)을 적용하려면, 벽체나 지붕 또는 바닥에 대한 전도시계열(Conduction Time Series (CTS)) 데이터가 필요하다. 이 수열의 계수 값들을 전도시계열 계수 (Conduction Time Series Factor (CTSF))라 부르기로 한다. Fisher 와 Spitler 등은 RTS 방법을 제안했으며, 라플라스 변환을 사용해서 CTSF 값들을 구했다1,2). RTS 방법의 중요한 가정 중 하나는 삼각함수처럼 일정한주기를 가지고 반복하는 상태 (periodic steady state) 이며, 이때 최대 냉방부하 계산의 주기는 24시간이다. Wang과 Chen은 CTSF를 구하는데 사용된 다양한 방법들에 대해 문헌조사를 했으며3), Z-transform4), State Space method5), Time Domain method6) 등이 사용된다고 발표했다. 또한 새로운 방법인 Frequency Domain Regression (FDR) 방법을 제안했으며, 이를 사용해서 복합체의 CTSF를 구했다. Spitler와 Nigusse는 Finite Volume Method를 사용해서 CTSF 를 구했다고 요약 보고했으며7), Nigusse 의 박사학위 논문8)을 참고 문헌에 인용했다. 발표된 서술은 다음과 같다. ‘층들을 정의한다. 각 층에 사용된 유한체적( Finite Volume)은 6개이고 시간 간격은 60초를 사용했다. 단위 삼각 온도 펄스를 외벽에 가한다음, 시스템의 펄스에 대한 반응도 (PRF) 를 계산한 후, 이를 전체열전달 계수 U로 나누어서 CTSF를 구했다.’7) 결과가 State Space method 와 잘 일치한다고 보고했으므로7), ASHRAE에서 발표한 결과들과 잘 일치하리라 추정된다. 그러나 요약 서술만을 비교해도, 이 논문에서 제안하려는 CTSF 계산 과정과 차이가 있다. Byun 은 유한차분법(Finite Difference Method)를 사용해서 CTSF를 계산하는 법을 제안했다9). 이를 ASHRAE 벽체 유형 24 (W24)와 지붕유형 14 (R14)에 적용한 결과들은 ASHRAE가 발표한 결과들과 잘 일치했다. 또한 반응 주기가 24시간보다 큰 경우에 대한 후속 연구가 필요하다고 제안했다. 실제 구조체의 반응주기가 24시간보다 긴 경우, 단순히 부하를 24시간 동안만 합산해서 구한 CTSF 값9)은 ASHRAE에서 발표한 CTSF 값과 일치하지 않았다.
본 연구에서는 벽체나 지붕재의 CTSF 값을 유한차분법으로 구하는 방법을 제안한 이전 연구 결과를, 열용량이 커서 반응주기가 24시간 이상이 되는 경우에도 적용할 수 있도록 일반화하려 한다. 따라서 이 연구의 목표는 이 논문에서 제안된 방법으로 계산된 CTSF 값이 ASHRAE에서 발표된 값과 잘 일치하는 것을 보이는 것이다.
2. 해석방법
2.1 시스템 모델 및 수치해석
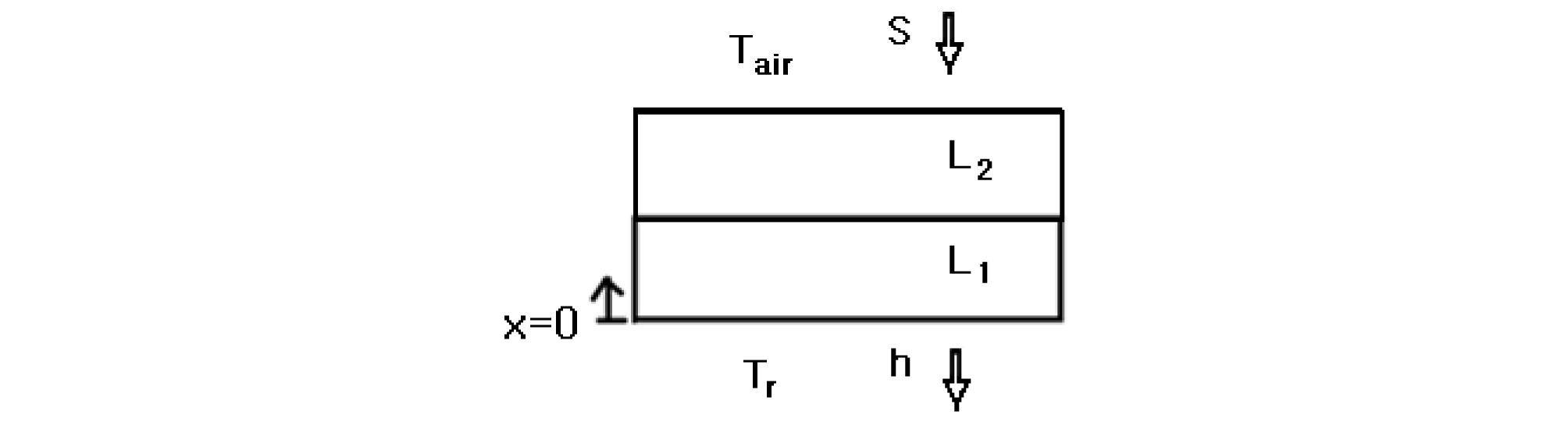
Fig. 1에 해석할 시스템과 좌표계가 제시되어 있다. 벽체나 지붕을 무한 평판으로 가정했다. 좌표계의 원점은 항상 실내공기 접촉면이다. 일반적으로 시스템은 다수의 층으로 된 복합체이다. 각 위치 및 시간에서의 온도 분포를 구하기 위해, 에너지 보존식을 적용해서 얻어진 모델식은 식(1)과 같다9,10,11,12).
| $$\frac{\partial T}{\partial t}=\alpha\frac{\partial^2T}{\partial x^2}$$ | (1) |
| $$T(x,\;0)\;=T_1$$ | (2) |
| $$-k\frac{\partial T(L,t)}{\partial x}=S$$ | (3) |
| $$-k\frac{\partial T(0,t)}{\partial x}=h(T(0,t)-T_r)=q_{room}^"$$ | (4) |
| $$-k_1\frac{\partial T_1}{\partial x_1}=k_2\frac{\partial T_2}{\partial x_2}$$ | (5) |
온도는 T, 열확산계수(Thermal diffusivity)는 α, 열전도 계수와 대류열전달 계수는 각각 k, h로 표시되어 있다. 식(2)는 초기 조건이고, 식(3)은 외기접촉면 L에서의 경계조건이다. 외기 접촉면에 작용하는 열유속의 세기는 S이다. 식(4)는 실내공기 접촉면에서의 경계조건이며, 실내로 전달되는 단위면적당 냉방부하중 전도에 의한 열유속이다. 실내공기 접촉면 온도를 먼저 구한 다음, 이를 식 (4)의 중간 항에 대입해서 냉방부하를 구한다. 복합 층인 경우, 고체와 고체 경계면에서의 열유속이 연속인 조건을 적용하면 식 (5)와 같다. 벽체나 지붕은 일반적으로 복합체이고 경계조건이 복잡하므로, 시스템을 다수의 층으로 분할한 다음, 임플리시트 유한 차분법(Implicit Finite difference method)을 사용해서 각 위치 및 시간에서의 온도 분포를 구했다.9,10,11,12) 다음 시점 (p+1) 에서의 온도 벡터T는 식(6)과 같이 표현할 수 있으며, 식(6)의 우변 항들은 현시점 (p)에서 결정되는 값들이다.
여기서 T는 온도벡터, A는 계수행렬, A-1은 역행렬이다. 따라서 초기치 (p=0)와 시간 간격 (∆t)이 주어지면, 식(6)의 우변 항들에 대한 값들이 계산되며 이는 곧 다음시점인 (p=1)에서의 온도가 된다. 식(6)의 좌변 값을 우변에 대입하는 과정을 마지막 시점까지 반복 적용해가면, 각 시점에서의 온도가 시간과 위치의 함수로 구해진다. 이와 같이 구한 수치해석 해를 엄밀해와 비교했으며, 잘 일치하는 결과를 얻었다9,10,11,12).
2.2 CTSF 를 구하는 수치해석 과정의 일반화
(1) CTS 와 CTSF 의 정의와 일반화
벽체 및 지붕에 대한 CTS 의 정의는 ASHRAE 핸드북에 의하면, 아래와 같다13).
| $$q_q=c_0q_{i,q}+{c_1q_{i,q-1}}+{c_2q_{i,q-2}}+\cdots\cdots+{c_{23}q_{i,q-23}}$$ | (7) |
여기서 24개의 ci는 conduction time series factors (CTSF)이고, i=0,23이다. 해당표면에서, qq는 기준시점 q에서의 시간당 전체전도부하이며 총 24개 항의 합이다. 기준시점부터 1 시간동안 입력부하는 qiq이고 기준시점으로부터 n시간 전부터 1시간 동안 입력부하는 qi,q-n이다. CTSF 값들은 ASHRAE 핸드북 13) 18장의 표 16~18에 정의된 조건하에서 계산되었으며, 자연수로 표시된 백분율 (%) 값이다. RTS 방법의 경우 최대 냉방부하 계산의 주기는 24시간이라는 것을 식(7)로 표현하고 있다1,2).
서술의 편의를 위해서 식(7)을 식(8)과 같이 일반화 하고, 반응주기를 Nhr로 표시한다. 반응주기는 총 부하를 구하기 위해 시간당 부하를 합산해야 하는 총시간이며, Nhr=24, 48, 72이다.
| $$q_q=c_0q_{i,q}+{c_1q_{i,q-1}}+{c_2q_{i,q-2}}+\cdots\cdots+{c_{Nhr-1}q_{i,q-(Nhr1-1)}}$$ | (8) |
만일 Nhr=24이면, 식(8)은 식(7)이 된다. CTSF의 수는 Nhr과 같다.
(2) 일반화된 CTSF 계산과정
참고문헌 [9]에 발표되어 있는 계산과정은 Nhr=24인 경우에만 유효하다. 벽체나 지붕재의 열용량이 커서, 반응주기가 1일보다 큰 경우를 위해 아래와 같이 일반화 시켰다. Nhr=48, 72는 각각 반응주기가 2일보다 작은 경우, 3일보다 작은 경우에 사용될 수 있다. 이 논문에서 CTSF는 ASHRAE 핸드북에 제시된 값, CTSF48과 CTSF72는 각각 Nhr=48, 72에서의 계산값, CTSF24는 CTSF48 또는 CTSF72를 24시간 반응주기로 변환한 값을 표시한다.
(Step 0) 단위시간 펄스란 용어를 다음과 같이 정의해서 사용한다: 해당시간 구간에서는 균일한 입력부하 S [W/m2]를 갖지만, 구간 밖에서는 입력부하가 0이다. 예를 들어 식(7) 좌변의 기준시점이 하첨자 q이면, 식(7) 우변의 첫 번째 항만 이고 나머지 (Nhr-1)개 항은 0이다. 만일 하첨자가 q=0이면 첫째날 0시부터 1시까지 매초당 입력부하는 S (시간당 총량 3600S)이고 첫째날 1시 이후의 입력부하는 0이다.
(Step 1)첫째날 0시부터 1시까지의 단위시간 펄스로 인해 실내로 전달된 시간당 냉방부하 Nhr개를 계산한다.
첫째날 0시부터 1시까지, 1시간 동안 단위시간 펄스를 경계조건 (3)에 입력한다. (Nhr+1)시까지 수치 해석 계산을 수행한 후 실내공기 접촉면에서 실내로 전달되는 시간당 냉방부하를 식(4)에 의해 1시간마다 구한다. 시간당 냉방부하 값들을 편의상 Gload(i)로 표시하자. 시간당 냉방부하의 시작 시간은 i이며 i=1,Nhr이다. Gload(i)는 첫째날 0시부터 1시까지 가해진 단위시간펄스로 인해, i시부터 i+1시까지 실내로 전달된 냉방부하이다. 따라서 Gload(24)는 첫째날 0시부터 1시까지 가해진 단위시간펄스로 인해, 24시부터 25시(다음날 0시부터 1시까지) 실내로 전달된 냉방부하이다. 만일 반응주기가 Nhr 시간이면, Gload(Nhr)=Gload(0)이다.
(Step 2)매시간 순 냉방부하인 값을 i=1,Nhr까지 계산한다.
는 시간 사이에 가해진 단위시간펄스가 냉방부하에 미치는 순수한 영향이다. 우변 첫 번째항은 시간 에 가해진 단위시간 펄스로 인해 실내로 시간 동안 전달된 냉방부하이다(S가 일정한 경우, 이 값은 GLoad(0) 과 같다). 우변의 두 번째 항은 시간 [0,1] (=첫째날 0시부터 1시까지)에 가해진 단위시간 펄스로 인해 실내로 시간 동안 전달된 냉방부하이다.
(Step 3) 반응 주기가 Nhr 시간이면, 이므로, 인덱스 i 값의 범위를 i=0,(Nhr-1)으로 변경한다. 따라서 i 는 1시간 간격이 시작하는 시간을 나타내는 인덱스이다. (Step 2)에 의하면,
| $$\triangle G(Nhr)={GLoad(0)}-{GLoad(Nhr)}$$ |
(Step 4) 로 표시된 매시간 순 냉방부하의 Nhr 시간동안 합을 구한다.
즉 G는 첫째날 0시부터 1시까지 가해진 단위시간 펄스에 의해, Nhr 시간 동안 실내로 전달된 총 냉방부하이다. 반응주기가 Nhr 시간 인 경우 이 값은 첫째날 0시부터 1시까지 가해진 단위시간 펄스의 총량인 3600S이다.
(Step 5) , i=0, Nhr-1 를 계산해서 CTSF48, CTSF72를 구한다.
Nhr=24인 경우 CTSF24로 표기해야 하나, CTSF24=CTSF가 성립한다는 것을 참고문헌 [9]에서 보였다. 한 시간 간격 의 시작을 나타내는 시간 인덱스는 I이다. ci는 첫째날 0시부터 1시까지의 단위시간 펄스로 인해 실내로 시간 동안 전달된 순 냉방부하의, 첫째날 0시부터 1시까지의 단위시간 펄스의 총량인 3600S에 대한 백분율이다. S가 일정하므로, 매시간 가해진 단위시간 펄스의 총량 또한 3600S이다.
(Step 6) CTSF24 변환 (Nhr=48, 72 인 경우 1일 주기로 환산)
에 ‘2일째’ 와 ‘3일째’ 날의 기여분을 더해서 재정의 한다. 즉,
(Nhr=48)
(Nhr=72)
를 CTSF24 (1일 주기로 환산한 CTSF)라 부른다.
RTS 방법은 1일을 주기로 가정하고 있으므로1,2), 제시된 계산과정이 맞으면 Nhr=48 또는 Nhr=72인 경우 CTSF24=CTSF가 된다. Nhr=24인 경우 CTSF24=CTSF이다9).
2.3 CTSF 계산용 입력데이타
Table 1에는 ASHRAE 2013 핸드북의 제 18장 표 16-1713)에 발표된 열용량(Thermal capacity), 열확산계수, 그리고 열저항(R value) 값이 결과 비교를 위해 요약되어 있다. (단위면적당) 열용량(Thermal capacity)은 질량과 비열의 곱을 면적으로 나눈 값이다[kJ/m2K]. ASHRAE 핸드북의 표 1813)에는 물성치 , 복합 벽체 및 지붕에 사용된 층들에 대한 코드번호와 각 층에 대한 자료, 예를들면 층 번호, 두께, 열전도율, 밀도, 비열, 열저항 값, 질량, 비열 및 참고 사항 등이 제시되어 있다. 대문자 F, G, I , M 는 각각 유체층, 외장재, 단열재, 그리고 벽돌 또는 콘크리트를 나타낸다. Table 1에 제시된 고체층의 갯수에 유체층 2개 (실내공기층, 외기층)를 더해야 전체 층수가 된다.
Table 1. Property summary of walls and roofs used for CTSF (ASHRAE 2005, 2013)13)
실내 공기층의 경우 벽체에는 F02 가 지붕에는 F03가 , 그리고 외기 층에는 F01이 사용되었다. F01, F02, F03 의 열저항은 각각 R=0.04, 0.12, 0.16 m2K/W이다.
핸드북에 제시된 열용량 값의 범위는, 벽체재인 경우 20.4~784.9 kJ/m2K이다. 최소값은 W2 (커튼월 그룹)이며 최대값은 W19 (벽돌그룹)이다. 콘크리트 그룹인 경우, 열용량의 범위는 83.8~631.6 kJ/m2K이다. 지붕재인 경우, 12.3~437.4 kJ/m2K이다. 최소값은 R3 (경사프레임 지붕)이며 최대값은 R18이다. 콘크리트 그룹인 경우, 134.9~437.4 kJ/m2K이다.
요약하면 ASHRAE 핸드북 자료에서 열용량이 가장 큰 재료는 , 벽체재의 경우 W19이며 지붕재의 경우 R18이다. 열용량이 가장 작은 재료는 W24와 R14이며 , 반응주기는 1일보다 작거나 1일 근처다. 이 경우 CTSF24 =CTSF임을 참고문헌 [9]에서 보였으므로, 다음절에는 열용량이 가장 큰 W19과 R18에 대한 결과만 발표 한다.
3. 결과 및 고찰
ASHRAE 핸드북에 제시된 CTSF 값을 계산할 때 사용된 입력값 들은 다음과 같다. 대류 열전달 계수 값은 실내의 지붕에서는 h=6.25 W/m2°C이고, 실내의 수직 벽체에서는 h=8.33W/m2°C이다. 외기 접촉면에서의 대류열전달 계수는 h=25 W/m2°C이다. 사용된 실내 온도 조건은 28℃이고, 외기온도는 35℃이며 일정하다.
2.1절에 서술된 수치해석과정을 사용해서, S=1000 W/m2의 조건에서 , 1분 간격으로 전진하며 (Nhr+1) 시간까지 층의 온도 분포와 실내로 전달된 열량(실내부하)을 구해나갔다. 이 논문의 첫 번째 목표는 CTSF와 CTSF24가 잘 일치하는 것을 보이는 것이다.
수치해석 방법의 정확성에 대해서는 선행논문에 발표되어 있으므로, 일부 요약만 하면 다음과 같다9). 24시간 동안 1분 간격으로 수치 해석을 해서 구한 결과들은 엄밀해와 잘 일치했다9). 고체 층에 대한 분할수를 증가시켜가며, 분할수의 영향을 시험했으며, 분할수의 영향을 받지 않는 값들이 표에 제시되었다. CTSF 값을 한자리수로 표현하는 경우, 분할수가 결과에 미치는 영향은 미미해서 상대적으로 적은 분할수로도 원하는 정확도의 결과를 얻을 수 있었다. 고체층의 초기 온도는 28℃가 사용되었으나, 이를 26℃, 35℃로 바꾸어도 한자리수 CTSF 결과에 영향을 주지 않았다.
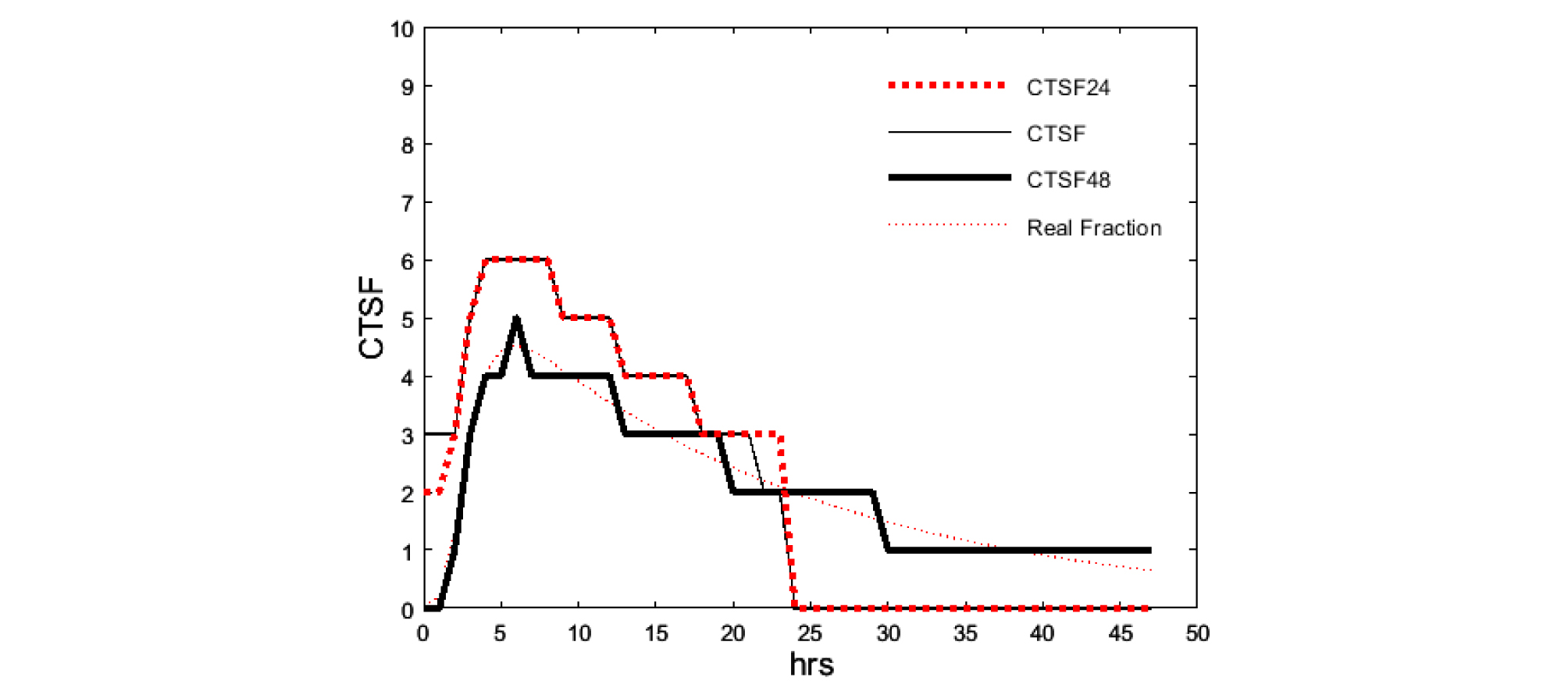
3.1 복합지붕 R18
Fig. 2에는 R18에 대한 CTSF 값들이 그려져 있다. Table 1에 제시된 바와 같이, R18 또한 R14처럼 4개의 고체 복합층과 2개의 유체층으로 구성되어 있다. R18의 경우, R14의 M11 (경량콘크리트) 대신에 M15 (중량콘크리트) 가 사용되었다는 점만 다르다. M15의 두께와 열용량은 각각 0.2032 m, 410.23 kJ/m2 이고, M11 경우는 각각 0.102 m, 108.95 kJ/m2이다.
Fig. 2에는 굵기가 다른 두 개의 실선과 두 개의 점선으로 결과가 표시되어있다. 가는 점선은 각시간당 부하를 4시간 부하의 총합으로 나눈 값이다. 48시간 전 펄스 입력부하가 24 시간 이후에도 영향을 미치고 있다. Fig. 2에서 가는 점선을 제외하고는, 유효숫자 한자리수 값이 그려져 있다. 굵은 실선은 CTSF48이며 가는 점선으로부터 생성되었다. 굵은 점선은 CTSF24이다. 가는 실선은 CTSF이며 ASHRAE 핸드북에 발표된 값들이다. 굵은 점선과 가는 실선이 잘 일치하고 있다. 초기 시간과 마지막 시간 근처에서 1% 오차는 반올림오차이다.9) 따라서 CTSF24와 CTSF는 잘 일치한다. CTSF 와 CTSF48 사이의 최대 오차는 3% 이며 초기시간대에 발생한다. RTS 방법의 가정하에서 CTSF 값을 사용하는 데는 문제가 없다.
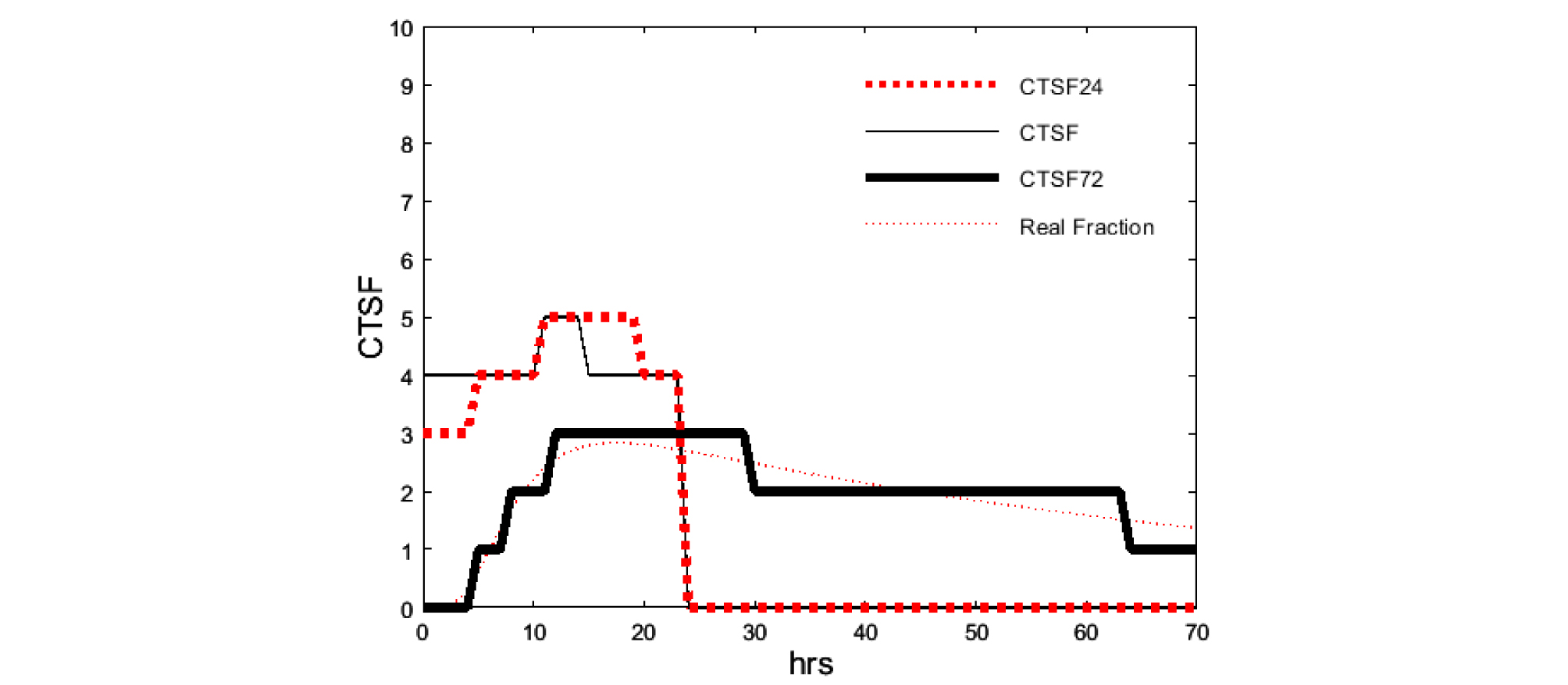
3.2 복합벽체 W19
Fig. 3에는 W19에 대한 CTSF 값이 그려져 있다. Table 1에 제시된 바와 같이, W19은 6개의 고체복합층과 2개의 유체층으로 구성되어 있다. ASHRAE 핸드북에 발표된 자료 중 열용량 값이 가장 크다.
Fig. 3에 사용한 선에대한 규약은 Nhr=48을 72로 바꾸면 Fig. 2와 같다. 가는 점선은 각시간당 부하를 72시간 부하의 총합으로 나눈 값이다. 72시간 전 펄스 입력부하가 24시간 이후는 물론 48시간 이후에도 영향을 미치고 있다. 굵은 실선은 CTSF72이며 가는 점선으로부터 생성되었다. 굵은 점선은 CTSF24이다. 가는 실선은 CTSF 이며 ASHRAE 핸드북에 발표된 값들이다. 굵은 점선과 가는 실선이 잘 일치하고 있다. 초기 시간과 마지막 시간 근처에서 1% 오차는 반올림오차이다9). 따라서 CTSF24=CTSF 이며 RTS 방법의 가정하에서 CTSF 값을 사용하는데는 문제가 없다. CTSF 와 CTSF72 사이의 최대 오차는 4%이며 초기시간대에 발생했다. 오차가 영향을 미치는 초기시간대가 Nhr=48인 경우보다 길어졌다.
위에 제시된 결과들은 벽체나 지붕재의 Nhr에 영향을 미치는 주요변수는 열용량이며, 열용량이 증가할수록 Nhr이 증가하는 경향을 보여주고 있다. 이 논문에서 제시된 방법을 사용해서 반응주기가 2, 3일인 경우에 대해서도 CTSF24를 구할 수 있으며, CTSF24=CTSF임을 보였다. 또한 반응주기가 4일 이상인 경우에도 제시된 방법을 확장 적용해서 CTSF24를 구할 수 있음을 추정할 수 있다. RTS 가정하에서, CTSF 값을 사용하면 된다.
4. 결 론
이 논문에서는 열용량이 큰 벽체 및 지붕재에 대한 CTSF 값을 유한 차분법으로 구하는 과정을 보였으며, 결과 요약은 다음과 같다.
(1) 벽체 및 지붕재의 반응 주기가 24시간 이상이 되는 경우, 단순히 부하를 24시간 동안만 합산해서 CTSF 값을 구하려하면, ASHRAE에서 발표된 CTSF 값을 구할 수 없다.
(2) 열용량이 큰 경우에도 CTSF24와 CTSF는 잘 일치했다.
(3) 새로운 벽체나 지붕재가 단일체는 물론 복합체여도, 이에 대한 CTSF 값을 제안된 방법으로 계산할 수 있다.
(4) 제안된 방법은 일반화되어 있으며, 간단하고, 명료하며, 필요시 유효숫자를 늘리기 쉽다.
(5) 제안된 방법의 경우, 생성된 CTSF 값들의 물리적 타당성을 쉽게 검증할 수 있다.