1. 서 론
최근에 발표된 국내 전력수급기본계획에서는 정격용량을 기준으로 국가 전원믹스에서 신재생에너지가 차지하는 비중을 2017년 약 9.7%에서 2030년 33.7%로 확대하는 계획을 제시하였다1). 이 정책에 대해 기후변화 대책, 미세먼지 저감, 탈핵 등에 부합한다는 긍정적인 평가와 함께 경제성, 기술적 요인 및 에너지 공급 안정성 등에 대한 우려도 함께 제기되고 있다. 전력공급원으로서 간헐성(intermittent) 특성은 재생에너지를 전통적인 발전원과 구분하는 대표적인 요소이다. 예를 들어, 풍력발전은 수시로 변하는 풍향이나 풍속 등에 의해 발전기 출력에 영향을 받아 전력계통시스템에서 전력부하에 대응하는 능력에 영향을 줄 수 있다. 이 같은 재생에너지의 특성을 대표하는 척도로는 이용률(Capacity Factor, CF)과 용량크레딧(Capacity Credit, CC)이 있다2,3).
CF는 발전기가 일정 기간 동안 최대 출력으로 연속 운전 시에 생산 가능한 전력량에 대한 실제 전력 생산량의 비율을 의미한다. 기후요소에 좌우되는 재생에너지의 CF는 전력계통시스템의 공급능력에 불확실성을 더하는 요소로 재생에너지가 전원믹스에서 차지하는 비중이 확대됨에 따라 전력시스템의 적정성(adequacy)에 영향을 미칠 수 있다. 전력시스템의 적정성은 전력수요를 충족시키는 전력시스템의 공급 능력을 의미하는데, 이를 나타내는 대표적인 척도로는 LOLP (Loss of Load Probability) 또는 LOLE (Loss of Load Expectation)가 있다. LOLP는 특정 시점에 가용 전력공급용량이 전력수요를 충족시키지 못할 확률을 그리고 LOLE는 특정기간 동안 전력 공급이 수요를 충족시키지 못한 기간의 길이(또는 확률의 합)를 의미한다4). 국내 전력시스템 현장에서는 적정성 척도로 LOLE가 이용되고 있으며, 국내 전원시스템의 특성을 이용해 도출된 LOLE (=0.3day/year)가 전력수급기본계획에서 이용되고 있다.
CC는 특정발전기 또는 발전원을 대상으로 정의되는데, 미리 설정된 LOLE 유지하면서, 이 발전기의 정격용량증가로 전력시스템에 추가될 수 있는 최대부하(maximum load)인 ELCC (Effective Load Carrying Capability)로 정의되거나 또는 추가된 정격용량대비 ELCC의 비율로도 정의된다5,6). 본 연구에서는 후자로 CC를 의미하기로 한다. 국내 전력현장에서 CC는 피크기여도라고 부르는데, 8차 전력수급기본계획에서는 국내 풍력발전의 CC를 0.019로 가정하고 있다1). 이에 따르면, 2030년까지 보급이 계획된 정격용량 17.7 GW에 대한 풍력발전의 실효용량은 0.336 GW (=17.7 × 0.019)에 지나지 않는다. 이 같이 CC는 경제성 평가, 최적 전원믹스 구성 그리고 예비력 수준 등에 중요한 역할을 하므로 적합한 CC의 추정은 전력시스템용량 중장기계획에서 매우 중요한 요소이다. 하지만 국내 전력시스템 현장에서 가정한 CC값의 구체적인 산정방법이 제시되어 있지 않아, 제시된 CC에 관해 관련 전문가 사이에 논란이 지속되고 있으며 이러한 논란의 원인 중 하나는 부족한 국내 풍력발전 CC에 관한 국내 연구 현실에서 찾을 수 있다7,8,9,10). 참고문헌7)에 주어진 풍력발전의 CC 연구는 제주도라는 지역적 범위 내에서 이루어졌고, 참고문헌8,9,10)에서는 국내 전체를 대상으로 하는 CC를 산정하였지만 단일 연도의 자료만이 이용되었다. 본 연구는 국내 풍력발전의 CC 산정을 위한 연구로서, 2011년 ~ 2017년 7개년 기간 동안의 시간별 풍력발전량과 용량에 관한 현실 자료를 이용하여 국외에서 제시된 CC 방법론을 적용한 결과를 비교한다. 또한 CC 산정에 필요한 CF의 추정에 있어 확률적 CF라는 새로운 방법을 제시한다. 아래에서는 CC 산정에 앞서 풍력발전의 시간별 CF에 대한 분석을 소개한다.
2. 이용률 분석
본 연구조사에 따르면, 국내 풍력발전에 관한 공식적인 자료원은 전력통계정보시스템(EPSIS)과 매년 한국에너지공단에서 발간하는 신재생에너지보급통계11)가 있다. 후자의 경우는 지역별로 구분되어 연도별 풍력의 보급용량 및 발전량 자료를 그리고 전자에서는 월별 지역별 발전량과 설비용량 자료를 제공한다. 이를 이용하여, 연구12)에서는 풍력발전의 월별 지역별 CF를 산정하고 비교하였다. 시간해상도(time resolution)가 시간인 풍력발전의 CF에 대한 연구도 이루어졌으나10), 분석에 사용된 자료가 단일년도라는 한계가 있다. 사실, 시간단위 발전량 자료가 공개되지 않는 현실로 인해 국내 재생에너지에 대한 시간단위 CF에 대한 연구는 매우 부족한 현실이다. 본 연구에서는 전력거래소로부터 2011 ~ 2017년 7개년 동안 연도별로 풍력의 발전량과 설비용량에 대한 시간단위 자료를 제공 받아, 연도별로 일 년 8760 (=365일/년 × 24시간/일) 시간대 각각에서의 CF를 계산하였다. 동일 연도에 속한 설비용량은 시점마다 다를 수 있으며, Table 1은 12월 31일 기준으로 CF 산정에 포함된 설비용량을 보여준다.
1)2016년과 같이 윤년이 있는 경우, 2월 29를 제외하여 모든 연도에 대해 8760시간 동일하게 적용
Table 1 Sample size in capacity (MW) for CF calculation by hour (12/31 in year)
| Year | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
| Sample Capacity | 491 | 556 | 647 | 710 | 916 | 1,117 | 1,284 |
1월 1일 오전 1시를 시간단위 1로 그리고 마지막 시간단위 8760은 12월 31일 24시로 하였을 때, 연도 y 그리고 시간단위 h의 CF CFMh,y는 다음과 같다.
| $$CF_{h,y}=\frac{wind\;generation\;at\;time\;h\;inyeary(MWh)}{365days\times24hours/day\times rated\;capacity\;at\;time\;h\;in\;year(MW)}$$ | (1) |
여기서, y=2011,..2017, h=1,2...,8760
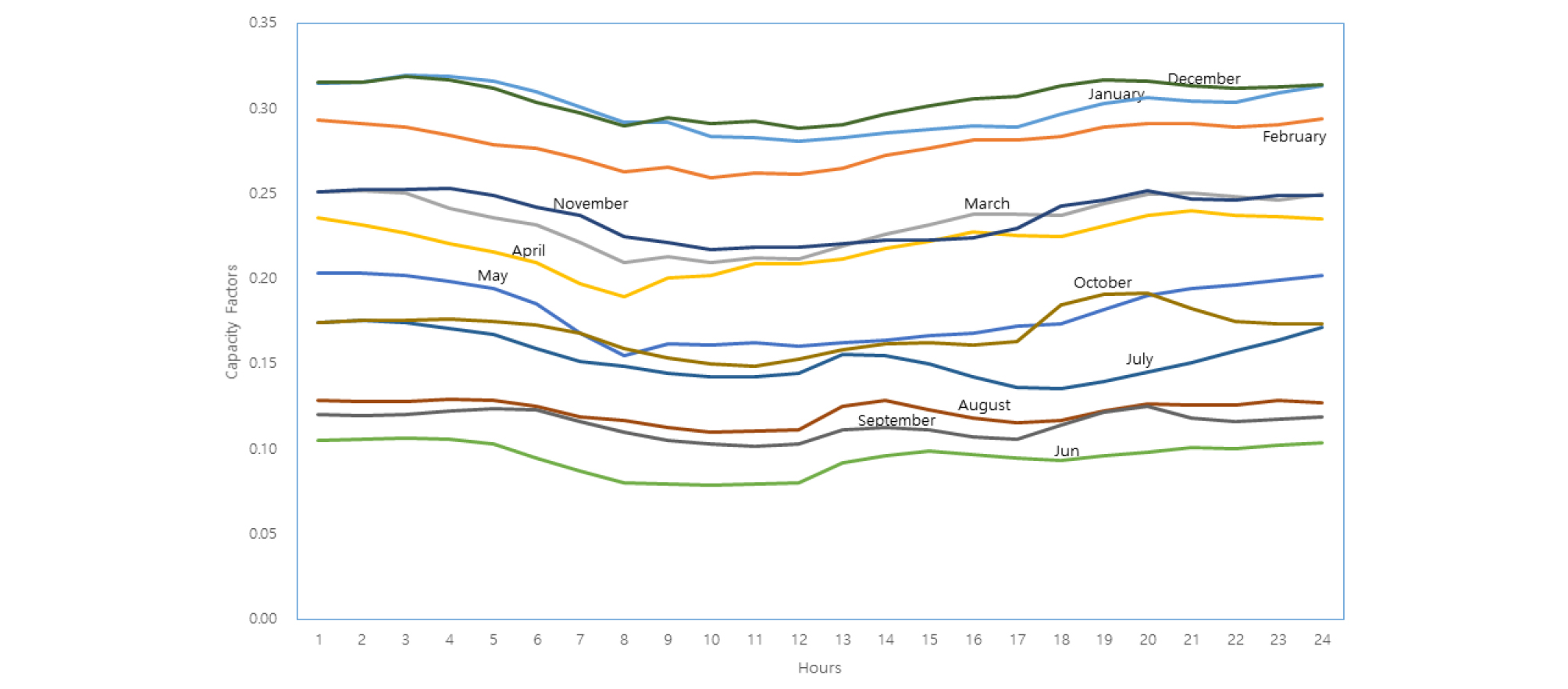
Fig. 1은 2011 ~ 2017년 7개년의 월별 시간별 평균 CF을 보여준다. 제시된 CF는 8760개의 시간대별 CF를 2011 ~ 2017년 연도별로 구하고, 월별로 동일한 시간의 CF값들을 평균하여 연도별 월별 시간대별 CF를 구하였다. 그리고 각 연도의 풍력설비용량 비율로 가중 평균하여 7년 기간에 대한 월별 시간대별 평균 CF를 구하였다. 그림에서 보듯이, 풍력의 CF는 12월과 1월 모든 시간에 걸쳐 다른 월에 비해 높은 값을 가지고 있다. 한편 가장 낮은 CF가 보이는 시기는 6월이며 9월이 그 뒤를 따르고 있다. 계절별로 CF 행태 특성을 보면, 겨울(12월, 1 ~ 2월)의 CF가 가장 높고 여름(6 ~ 8월)의 CF가 가장 낮았다. 여기서, 봄은 3 ~ 5월 그리고 가을은 9 ~ 11월로 정하였다. 시간별 CF의 변화 특징을 보면, 오전 10시에서 12시 사이의 CF값이 하루 중에서 가장 작은 값을 그리고 밤 시간대 CF가 높은 CF 값을 가지는 것으로 조사되었다.
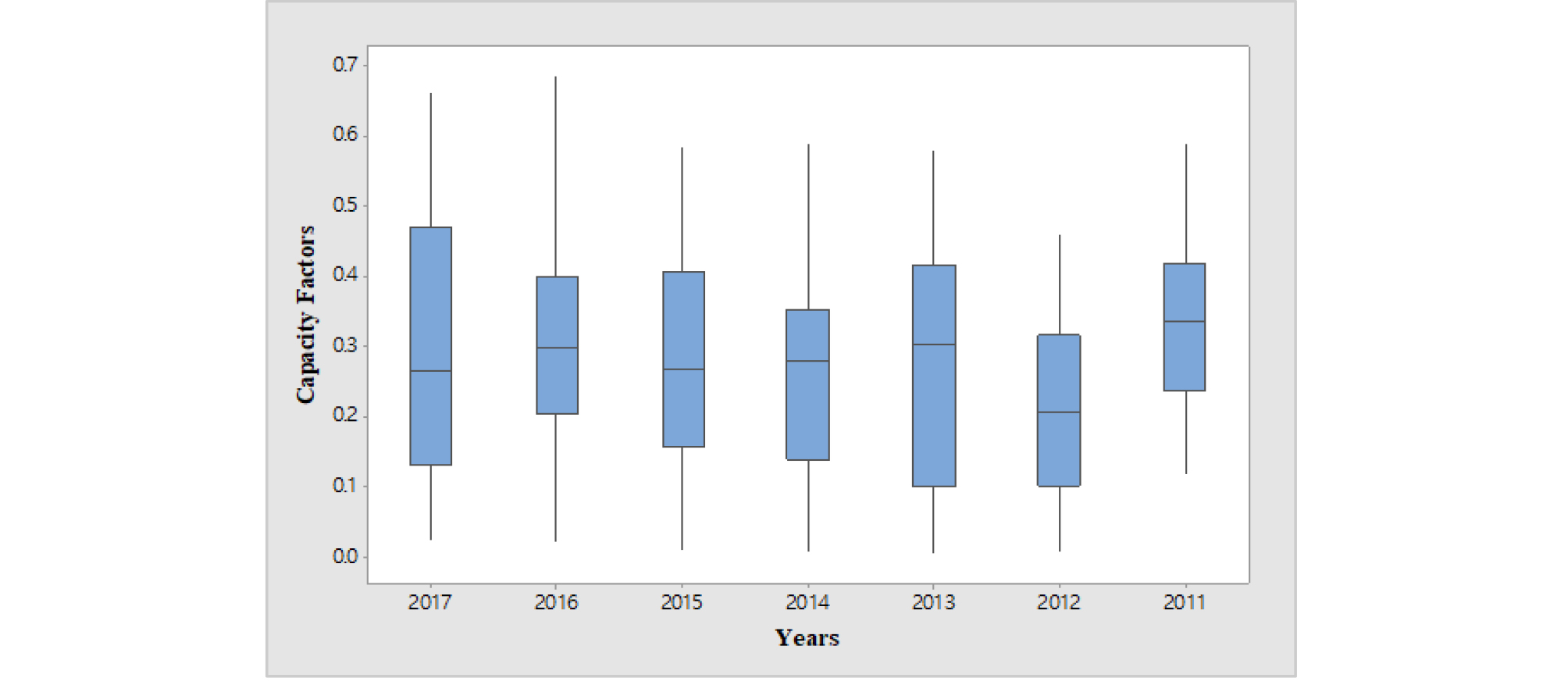
Fig. 2는 풍력발전 CF의 변동성(variability)을 살펴보기 위해 최대전력부하가 발생하는 전형적인 시점을 알려진 1월 오전 11시 CF 표본 31개에 대한 Box-Plot을 연도별로 나타내었다. 그림에서 보듯이, 특정 연도 내에서뿐만 아니라 연도별로도 의미 있는 CF 변동성을 확인할 수 있다. 따라서 복수 연도의 CF값을 이용할 때, 서로 다른 연도에 속한 CF의 단순평균은 일종의 완화(smoothing) 효과로 인해 CF의 변동성이 과소평가될 수 있음에 유의해야 한다.
3. 용량크레딧 분석
CC 산정방법은 크게 신뢰성기반 방법과 CF기반 근사화 방법으로 구분된다5,6,13). 전자는 전력부하와 발전기의 정지(outage)에 관한 동태적 특성을 CC 산정에 고려하는 방법으로서, 가장 이론적 근거가 충실한 방안으로 인식되고 있다. 이 방법의 결과물이 ELCC가 되기 때문에 ELCC 방법이라고 한다14). CF기반 방법은 특정 시간대에 속하는 CF값들의 평균으로 CC를 산정하는데, 필요한 자료가 비교적 작고 산정 과정이 간단하다는 장점이 있지만, 전력부하 및 전력시스템의 동태적 특성 등을 반영하지 못하는 한계를 가지고 있다. 이러한 이유로 이것은 소위 ELCC방법에 대한 근사화 방법으로 취급된다. 참고문헌13)에서는 CF기반 방법으로 국내 태양광의 CC를 산정하였으며, 연구10)에서는 ELCC방법으로 풍력발전의 CC를 제시하였다. 하지만 후자에서는 단일 연도(2014년) 전력부하 및 시간단위 CF 자료가 이용되었다. 본 연구에서는 복수연도의 풍력발전의 CF자료를 이용하여 소위 확률적 CF를 도입하고 이를 이용하는 새로운 CC 산정방법을 제시한다.
3.1 CF기반 방법
CF기반 방법은 시간대별 CF가 확정적(deterministic)으로 주어진 상태에서, 연도 y의 CC (CCy)는 특정 시간대들의 집합 Ty에 속한 시간대 CF들의 평균으로 정한다6,15). 즉,
| $$CC_y=\frac{\sum_{h\in T_y}CF_{h,y}}{\left|T_y\right|}$$ | (2) |
여기서, Ty는 전력부하가 높은 시간대들의 집합으로, 집합 Ty의 적정 규모에 대해 문헌에 제시된 것은 없으나, 일부 문헌에서는 전체 표본의 수 8760개의 10%로 하는 것을 제안하고 있다15). Table 2는 이 방법을 통해 구한 CC를 보여준다. CC 대표 값은 각 연도의 CC값에 풍력설비용량비율을 가중 평균하여 구하였다. 전력부하의 상위 10%인 경우 CC에 대해 2011 ~ 2017년 7개년 CC 대표 값은 0.2301이다.
Table 2 Capacity credits of wind power by year: deterministic CF-based simple average method
위 방법은 피크부하 시간대 CF들을 CC 산정에 반영하고 있지만, 여러 시간대들의 CF들을 단순 평균하여, CF의 변동성을 고려하지 못하는 한계를 가지고 있다. CF의 변동성을 CC산정에 반영하기 위해 CF를 상수가 아닌 확률변수로 취급하여, CF가 특정 값보다 작은 값을 가질 확률 α가 주어졌을 때, 이 특정 값을 신뢰도 (1-α)100% 하의 CC라고 칭하기로 한다. 만약, 확률변수 CF의 확률분포(distribution function) F(x)가 알려져 있다면, 신뢰도(1-α)100% 하의 CC는 F-1(α)가 된다. 아래에서는 이렇게 CF를 상수가 아닌 확률변수로 취급하는 것을 확률적 CF 방식이라 부르기로 한다. 확률변수 CF에 관한 특성 추출은 CF 표본에 의존할 수밖에 없는데 짧은 풍력 발전의 역사로 인해 8760개에 이르는 시간대별로 유의한 통계적 분석이 가능한 수준의 충분한 수의 표본을 확보하는 것은 거의 불가능하다. 따라서 국내외 연구에서는 전력부하를 고려하여 복수 연도 또는 여러 시간대들의 표본들로 통계적으로 유의한 CF 표본집단을 구성하고, 이 표본집단의 통계적 특성을 통해 CC를 산정하였다13,16).
CF의 확률분포가 특정되지 않은 경우는, 주어진 CF 표본들의 백분위수(percentile)를 CC로 정하였는데, 이 때 CF 표본집단의 구성은 문헌에 따라 다양한 방법이 제시되고 있다. 참고문헌4)에서는 특정 연도의 전체 시간대에서, 전력부하가 상위 10%에 드는 시간대의 CF들로 이루어진 표본집단을 연도별 구성하였다. Table 3은 이렇게 설정한 표본집단을 대상으로, 다양한 백분율에 대응되는 백분위수 값을 보여주고 있다. 백분위수 값이 연도별로 주어지며, 7개년(2011 ~ 2017년) 전체 표본에 대한 CC 대표 값은 7개년도 백분위수 값에 대해 연도별 설비용량 비율로 가중평균으로 정하였다. α=0.5인 경우의 CC (=0.2058)를 전력부하가 상위 10%인 경우의 확정적 CF기반 방법에 의해 산출된 CC값(=0.2301)과 비교하면 작다. CC는 α값에 대해 증가함수이기 때문에 확정적 CF기반 방법은 0.5보다 다소 큰 α값으로 산정된 확률적 CF기반 산정 결과에 비견될 수 있음을 시사한다.
Table 3 Capacity credits of wind power by year: probabilistic CF-based method using sample percentiles
위에서 소개된 방법에서는 CF 표본집단의 구성이 연도별로 이루어져 풍력 출력이 하루 내에서 변동하는 특성을 반영할 수 없고, 확률적 특성을 반영함에 있어 분명한 한계를 가진 표본집단의 백분위수로 CC를 구하고 있다. 또한, 전력부하가 높은 시간대의 CF들은 CC 산정에 모두 동일한 중요도가 부여되어 피크부하의 시간대들에 대한 별도의 고려가 허용되지 않는다.
본 연구에서는 시간별 CF의 확률적 특성을 분석하기 위해, 2011 ~ 2017년 7개년 CF 표본들을 월별로 그리고 시간별로 표본집단을 구성하였다. 아래에서 월과 시간의 조합을 타임블록이라고 부르기로 한다. 타임블록별로 표본의 수는 다른데, 예를 들어 일(day)의 수가 31일인 1월 11시에 대응되는 타임블록의 표본의 수는 217개(=31일/년 × 7년)이다. 타임블록별 표본을 이용하여 대응되는 확률변수 CF에 통계적으로 적합한 분포를 탐색하였다. 탐색에는 통계 패키지 MINITAB ver. 18이 사용되었으며, 유의수준(significance level) 95% 하에서 적합성 검증은 Anderson-Darling 통계량을 사용하여 계산된 P 값을 기준으로 하였다. 정규분포를 포함하여 복수의 분포들이 적합하면, 정규분포를 선택하였으며, 그렇지 않은 경우에는 P값이 가장 큰 분포를 선택하였다. 통계적으로 유의한 특정 분포를 규정하지 못하면, Box-Cox나 Johnson 변환을 통해 정규화가 가능한지 검토하였다17). 288개의 타임블록에서 와이블(Weibull)분포를 따르는 블록의 수는 152개로 가장 많은 부분을 차지했고 그리고 정규분포가 타임블록의 수 122개로 그 뒤를 따랐다. 그리고 3개의 타임블록의 경우는 원 표본에 적합한 분포를 규정하지는 못하였으나 Johnson변환을 통해 정규화가 가능하였는데, 예를 들어 6월 11시에 대응되는 타임블록의 변환함수는 1.69721 + 0.642711 × Ln ((X- 0.000124710)/ (0.620244-X))이다. 그리고 288개의 타임블록 중에서 11개 타임블록 대해서는 통계적으로 유의한 확률분포를 찾지 못하였다.
확률분포가 규정된 타임블록(t,m)의 누적분포함수(cumulated distribution function)를 F(t,m)(•)으로 표시한다. Table 4는 α=0.1일 때, 각 타임블록의 백분위수를 나타낸 것으로, 분포가 규정된 타임블록의 백분위수는 역누적분포함수 로, 그렇지 않은 타임블록의 경우는 표본들로부터 백분위수로 구하였다. 타임블록 (t,m)에 대응되는 백분위수값을 으로 표기하고, w(t,m)을 타임블록 (t,m)에서 피크부하가 발생할 확률이라고 하면, 신뢰도 (1-α)100% CF로 산정된 CC는 다음과 같다: .
Table 4 Percentiles by time block: using probability distributions (α=0.1)
타임블록 (t,m)에서 피크부하가 발생할 확률을 추정하기 위해서 연도별로 전력부하가 상위 10%안에 드는 타임블록을 2011 ~ 2017년 7개년 자료를 누적하고, 타임블럭별로 상대적 비율을 산정하였다(Table 5). 표에서 보듯이, 겨울과 여름의 비율이 각각 0.64와 0.29로 다른 계절에 비해 절대적인 비중을 차지하고 있으며, 겨울은 오전 10-11시 비중이 그리고 여름은 오후 3-4시의 비중이 다른 시간대보다 높음을 확인할 수 있다. Table 6은 신뢰도(1-α)100% CF값으로 산정된 CC를 보여준다. 이에 따르면, 8차 전력수급기본계획에서 제시된 풍력발전의 피크기여도 0.019는 신뢰도가 95% 하의 CF값으로 산정된 CC (0.0188)로 해석될 수 있어, 상당히 보수적인 기준이 풍력 CC 산정에 적용되었음을 짐작케 한다.
Table 5 Ratio of power load by time block in the top 10% peak load (2011 ~ 2017)
Table 6 CC calculation of wind power: using distribution percentile
| α | 0.05 | 0.10 | 0.15 | 0.20 |
| Capacity Credits | 0.0188 | 0.0573 | 0.0865 | 0.1104 |
3.2 ELCC 방법
CF기반 방법은 과정이 간단하고 필요한 자료의 규모도 상대적으로 작다는 장점이 있지만, (확정적 또는 확률적) CF와 정태적인 전력부하만이 CC 산정에 반영되어, 전통적인 발전원의 정지와 전력부하의 동태적인 특성을 반영하는데 한계를 가지고 있다. 더구나, 재생에너지가 전력믹스에서 차지하는 비중에 따른 영향을 CC 산정에 반영할 수 없다. 즉, CF기반 방법이 제시하는 CC 값은 풍력발전 보급 용량에 관계없이 항상 일정하다. 이 같은 CF기반 방법의 문제점을 어느 정도 극복할 수 있는 방법이 ELCC 방법이다. 본 연구에서는 전력시스템의 적정성을 나타내는 척도로 국내 전력수급기본계획에서 사용하는 LOLE 값 0.3 day/year을 가정한다.
아래에서는 LOLE를 구하는 방법을 포함한 ELCC 방법에 대해 간단히 소개한다. 먼저, LOLE는 다음과 같이 계산 된다: , 여기서 Gt는 t시점에 전통적인 발전원의 가용용량(MW), lt는 전력부하(MW)를 각각 의미하며, FG(x)는 전통적인 발전원의 가용용량의 누적확률분포함수를 나타낸다. 마지막으로 T는 연간 기간의 총수를 의미한다. 이 같은 LOLE를 계산하기 위해서는 확률변수 Gt의 누적분포함수 FG(x)가 주어져야 한다. 가용용량 Gt는 주어진 정격용량에서 정지용량(outage capacity)을 차감하여 결정되는데, 각 발전기의 상태(state)가 작동(On)과 정지(OFF) 등 두 가지로만 구분되고, 개별 발전기들의 정지확률이 서로 독립이라는 가정 하에 가능한 정지용량 각각에 대한 발생 확률 값을 계산할 수 있다18). 이 때 발전기의 정지는 계획정지와 비계획정지로 구분될 수 있으며, 이들의 발생은 서로 독립적이라고 가정한다. lm을 최대부하(maximum load)라고 표기하면, 최대부하 대비 t시점 부하 lt의 상대적 크기를 gt (=lt/lm) 로 표시하고, 를 부하패턴(load pattern)이라고 부른다.
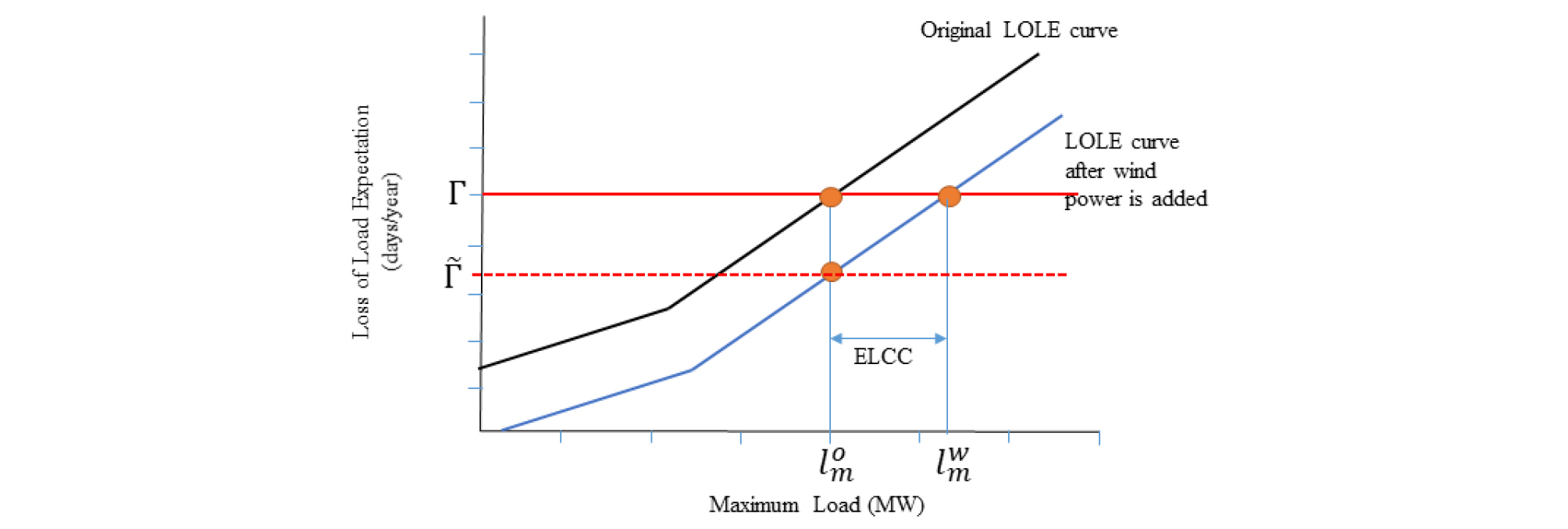
ELCC를 구할 때, 부하패턴은 고정시키고 최대부하를 조정하여 목표 신뢰도를 만족하는 부하를 구한다. ELCC 산정을 위한 첫 번째 단계에서는, 풍력발전을 제외한 전통적인 발전원만으로 구성된 전력시스템의 적정성 목표로 설정된 LOLE 값 를 만족하는 최대부하 결정한다. 즉, . 다음 단계에서는, 풍력발전이 포함된 전력시스템에서 LOLE를 구한다. 이 시스템에서 전통적인 발전원이 담당하는 부하는 풍력 발전량만큼 감소하게 된다. t시점의 풍력 발전량(또는 부하 감소 기여분)을 라고 하자. 여기서 Q는 풍력발전 설비용량을 그리고 cft는 t시점의 이용률이다. 부하패턴 {gt}와 최대부하 가 주어져 있는 상태에서, 풍력이 포함된 경우의 LOLE 값(Fig. 3에서 으로 표기)을 계산한다. 누적분포함수의 특성으로 인해, 는 풍력이 포함되기 전의 LOLE값보다 작거나 같다(). ELCC 계산의 세 번째 단계에서는 가 되는 최대부하를 찾는다. 이를 라고 표시하자. 그러면 ELCC는 로 구할 수 있으며, CC는 가 된다.
ELCC 방법을 위해서는 먼저, 기준시스템(reference system)이 설정되어야 한다. 전력시스템에 풍력의 포함 전후에 적정성의 차이를 비교하기 위한 기준시스템은 전통적인 발전원만으로 구성되는데, 2017년 국내 전력시스템에서 열병합발전기와 신재생에너지 등을 제외한 대부분의 발전기가 포함되었다. 각 발전기 타입은 개별 발전기의 용량에 따라 다시 하위그룹으로 분류하였는데, 원자력은 용량이 서로 다른 6개의 하위 그룹이 있으며, 원자력 발전소의 총 개수는 24대이다. 기준시스템에 포함된 전체 발전용량은 94,115 MW로 2017년 말 국내 발전설비용량의 80.5%에 해당되는 규모이다19). 기준시스템에는 발전원의 용량 및 정지확률 등이 함께 주어진다. 특히, 발전원별 정지(계획정지+비계획정지)확률은 월별로 주어지며 2011 ~ 2017년 평균값을 이용하였다. 주어진 기준시스템을 이용하여, 앞에서 언급된 가용용량의 확률분포 FG(x)에 관련된 전력시스템의 정지확률표(COPT, Capacity Outage Probability Table)를 월별로 계산하였다18).
LOLE를 구하기 위해서는 COPT와 함께 시간대별 전력부하가 요구된다. 본 연구에서는 연도별로 최대부하를 구하고 이를 해당연도의 시간대별 부하로 나누어 부하패턴(load pattern)을 연도별로 생성하였다. ELCC는 풍력발전이 포함되지 않은 전력시스템과 풍력발전 도입으로 목표 수준의 LOLE를 만족하면서 전력시스템에 추가될 수 있는 부하수준을 비교해서 산정된다. 따라서 풍력발전 용량에 따른 풍력의 시간대별 발전량 자료가 필요하다. 아래에서는 시간대별 발전량을 결정함에 있어 기존의 확정적 CF를 사용하는 경우와 본 연구에서 도입한 확률적 CF를 사용한 경우를 비교한다.
Table 7은 기존의 방법에 따르는 산정결과로, 시간대별 확정적 CF자료를 이용하여 풍력의 보급용량에 따른 CC를 연도별로 산정한 결과를 보여준다. 표에서 첫 번째 열은 기준시스템 전체 용량 94,115 MW 대비 풍력발전의 보급 비율을 나타낸다. 마지막 열은 2014 ~ 2017년 4개년의 설비용량에 따른 가중평균을 나타낸다. 풍력발전의 보급 비율이 증가함에 따라 CC가 감소하는 특성은 다른 문헌의 결과와 유사하다2,5,6). 한편, 기존 국내 연구에서 제시된 CC와 그리고 Table 7에 주어진 CC 모두는 약 0.18 ~ 0.3의 범위에 포함된다7,8,9,10). 하지만 이 값은 국내 전력수급기본계획에서 이용되고 있는 피크기여도 0.019와 비교하면, 매우 큰 차이를 보인다.
Table 7 CC Calculation by ELCC method: using deterministic CF
Table 8은 시간대별 확정적 CF를 대신하여, 신뢰도 90% 하의 타임블록별 확률적 CF를 이용한 ELCC 방법을 통해 CC를 산정한 결과를 보여준다. 이 때, 동일한 타임블럭에 속한 시간대의 CF는 모두 같다고 가정한다. 즉, . 왼쪽에서 2번째 ~ 7번째 열은 풍력발전의 보급률에 따른 연도별 CC이고 마지막 열은 2011 ~ 2017년 CC의 단순 평균값으로, Table 7과는 다르게, 타임블록별 CF가 복수연도의 표본들로 부터 생성된 사실을 고려하였다. Table 9는 신뢰도(1-α)100%에 따른 CC값의 변화 모습을 보여준다. 여기서 CC는 주어진 신뢰도 하에서 보급 용량에 따른 CC를 연도별로 구하고, 이를 2011 ~ 2017년 7개년 값을 평균한 것이다. 2017년 국내 풍력의 보급률과 가장 가까운 비율인 2%인 경우를 기준으로 할 때, 8차 전력수급기본계획에서 제시한 0.019는 90 ~ 95% 신뢰도에 대응되는 CC 값으로 해석될 수 있다.
Table 8 CC Calculation by ELCC method: using probabilistic CF (α=0.1)
Table 9 Comparison of CC by probabilistic CF based ELCC by reliability level
4. 결 론
특정 발전원의 정격용량 중에서 최대전력수요를 감당하는 비율을 나타내는 CC는 발전원의 실효용량을 결정하기 때문에 전력수급기본계획을 포함한 중장기 발전용량계획에서 필요한 중요한 요소 중 하나이다. 하지만 풍력을 포함한 재생에너지의 국가 단위 CC에 대한 국내 연구는 매우 미진한 상태이다. 본 연구는 풍력발전의 용량크레딧(CC) 산정에 관한 연구로서, 국내 풍력발전의 CC 산정을 위해 2011 ~ 2017년 7개년 동안의 국내 풍력발전량에 대한 시간대별 자료를 활용하였다.
국내외 문헌에서 제시된 CC 산정을 위한 대표적인 방법인 CF기반 방법과 ELCC 방법에 본 연구에서 제시한 새로운 확률적 CF 개념을 적용하였다. 이 개념은 월별 시간별로 정의되는 타임블록별로 통계적으로 적합한 확률분포를 통해 특정 신뢰도 수준하의 CF를 생성하여 이를 CC 산정에 이용한다. 먼저, CF기반 방법에 확률적 CF를 적용한 본 연구의 결과와 소위 확정적 CF를 적용한 기존 연구결과를 비교하였다. 본 연구에서 제시한 CF기반 방법에서는 확률변수로서 CF의 변동성을 고려할 뿐만 아니라 피크부하가 발생하는 시간의 가중치를 CC 산정에 반영하였다. 산정결과에 따르면, 8차 전력수급기본계획에서 제시된 값 0.019는 신뢰도 95%하의 CF기반 방법에 의한 CC 값(0.0188)으로 근사적으로 해석될 수 있다.
발전기의 정지 및 전력부하의 동태적 특성을 반영하고 풍력발전의 보급용량에 따른 영향을 평가할 수 있는 ELCC방법에 본 연구에서 제안된 확률적 CF개념을 적용하였다. ELCC방법을 위한 기준시스템은 2017년 국내 전력시스템의 전체를 대표할 수 있는 규모로 하였으며, 월별 계획 및 비계획 정비확률을 사용하여 획득 가능한 가장 세밀한 정지특성 자료를 CC 산정에 이용하였다. 풍력발전의 보급이 확대됨에 따른 CC의 변화를 다양한 신뢰도하에서 기존의 확정적 CF를 사용하는 경우와 확률적 CF를 사용하는 경우를 비교하였다. ELCC방법에 의한 CC 산정결과에 따르면, 국내 8차 전력수급기본계획에서 전제한 풍력발전의 CC 값은 90% ~ 95% 신뢰도에 대응되는 CC로 해석될 수 있다. 본 연구에서 사용한 CF는 지역별 구분이 없는 것으로 CC의 지역적 차이를 규명할 수 없다. 따라서 지역별로 구분된 CC에 대한 연구가 추후에 필요할 것으로 판단된다.