1. 서 론
2. 유한 요소 모델
2.1 대면적 양면형 태양광 모듈 구조
2.2 기계적 물성 및 유한요소 모델
2.3 경계조건
3. 실험 설계
3.1 실험계획법
4. 결과 및 고찰
4.1 구조해석 결과
4.2 주효과도 분석
4.3 반응표면법을 이용한 분석
4.4 최적화 모델 검증
5. 결 론
1. 서 론
최근 전 세계적으로 태양전지 제조에 사용되는 웨이퍼의 대면적화를 위한 개발이 가속화되고 있다. 웨이퍼를 대면적화할 경우 단위 생산량 및 출력 증가하며, 모듈 제조 시 동일 면적을 상대적으로 적은 수의 셀로 구성할 수 있어 각 셀에 요구되는 전기부품 및 조립시간이 감소해 제작비용을 줄일 수 있는 장점이 있다. 2019년 이전 웨이퍼 시장점유율 80% 이상이 M2셀이었으나, 2021년에는 M6셀이 42%, M10셀이 27%, 2022년 2분기를 기준으로는 M10셀이 50% 이상으로 예측되면서 대형 실리콘 웨이퍼의 시장점유율이 급속하게 증가하고 있는 추세이다1). 또한 웨이퍼가 대면적화 됨에 따라 고출력 모듈에 대한 수요를 맞추기 위해 대면적 태양전지를 집적한 모듈화 개발이 진행되며 모듈의 크기도 점차 증가하고 있는 실정이다2).
그러나 태양광 모듈(Photovoltaic module, PV module)의 크기가 증가할수록 무게가 증가하므로 기존 상용 알루미늄 프레임을 적용해 설치할 경우 풍압, 적설압 및 자중에 의해 모듈에 처짐이 발생할 가능성이 있다. 모듈이 하중에 의해 변형되면 모듈 내 균열 또는 리본의 박리가 발생할 수 있으며, 셀 내부 크랙 및 파손으로 인해 데드 셀(Dead cell)이 증가할 수 있다. 이는 모듈의 충진률과 변환효율 감소의 원인이 된다3,4).
국내외적으로 기계적 하중에 따른 모듈 변형 거동 및 형상최적화에 대한 연구가 진행되고 있다. Hartley et al. (2020)5)은 단면형과 양면형 태양광 모듈에 대해 재하실험과 유한요소해석(Finite element analysis, FEA)의 비교 검증을 통해 3차원 유한 요소 모델을 개발하고 모듈 변형에 영향을 미치는 주요 매개변수를 도출하였다. Noh et al. (2022)6)은 단면형 대면적 태양광 모듈에 대해 유한요소해석과 기계적 하중 시험을 통해 모듈 변형 및 셀 파손 경향을 분석하였다. Tummalieh et al. (2021)2)은 단면형 대면적 태양광 모듈에 대해 기계적, 광전기적 그리고 비용 및 수명 측면에서 적합한 프레임 형상을 제시하였다.
한편 웨이퍼 대면적화와 더불어 양면형 셀과 모듈에 대한 개발이 빠르게 진행되고 있다. 현재 양면형 셀의 경우 후면 효율이 전면 효율의 60%에서 최대 90% 수준까지 도달할 수 있다7). 또한 양면형 모듈의 경우 단면형 모듈에 비해 생산비용은 다소 증가하지만, 에너지 생산은 1.25 ~ 1.3배까지 증가할 수 있다는 장점이 있다8,9,10). 2020년 양면형 셀은 시장점유율 20%로 집계되었으며, 2030년에는 70%까지 상승할 것으로 예측된다. 양면형 모듈은 2020년 시장점유율 12%이며, 2030년에는 30%까지 증가할 것으로 전망된다11).
양면형 모듈은 후면이 유리로 되어있어 단면형 모듈에 비해 상대적으로 중량이 크다. 따라서 대면적화 할 경우 자중에 의해 프레임이 변형되어 모듈에 처짐이 발생할 가능성이 높다. 그러나 대면적 양면형 태양광 모듈 프레임의 형상최적화에 관한 연구는 미비한 실정이다.
따라서 본 연구에서는 유한요소해석을 통해 대면적 양면형 태양광 모듈의 처짐량을 분석하고 반응표면법(Response surface methodology, RSM)을 활용하여 모듈의 처짐량과 프레임 중량이 최소가 되는 태양광 모듈 프레임 형상을 제시하고자 하였다.
2. 유한 요소 모델
2.1 대면적 양면형 태양광 모듈 구조
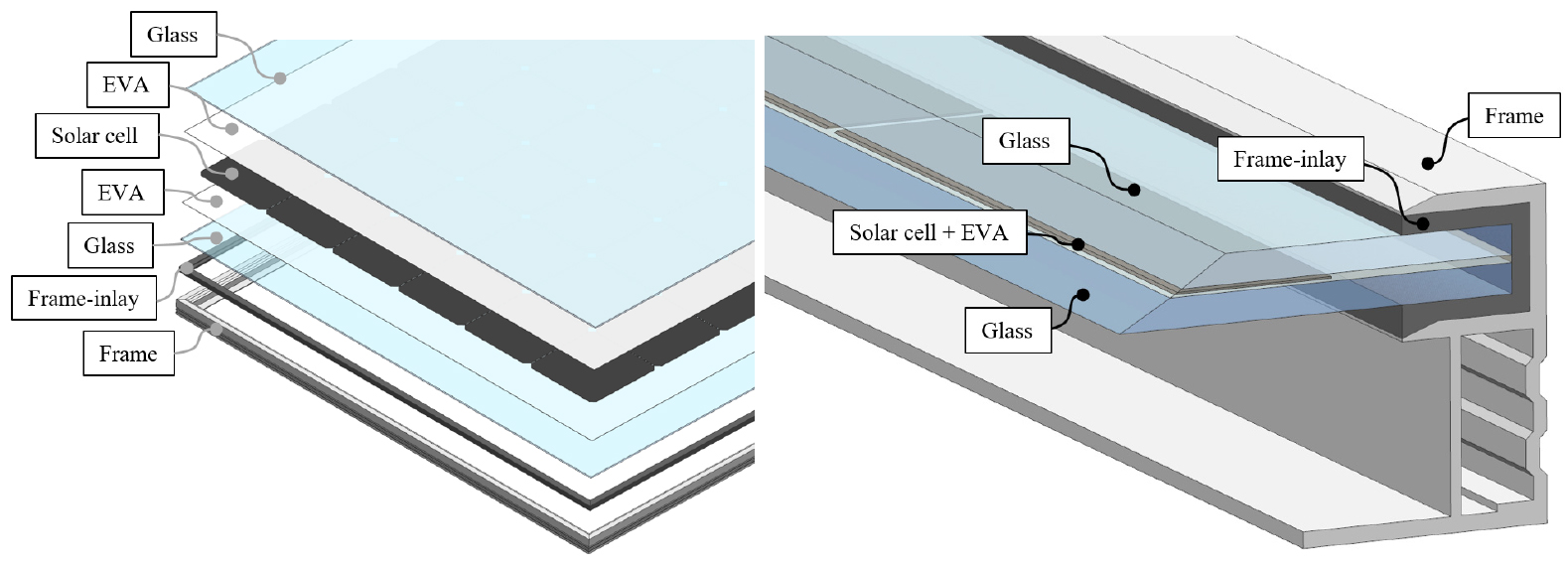
대면적 양면형 태양광 모듈 프레임 형상최적화를 위해 M10 셀(182 × 182 mm2)이 총 78개(6 × 13)가 배열되는 585 W 급 양면형 태양광 모듈을 참고하였다12). 모듈 구성 요소는 Fig. 1과 같이 셀(Silicon), EVA, 유리, Frame (Al), Frame-inlay로 이루어져있으며, 각 구성요소의 두께는 Table 1과 같다. 셀 두께는 0.18 mm로 선정하였고 라미네이션 후 두께는 0.8 mm로 하였다13). 양면에 배치된 유리의 두께는 3.2 mm, Frame-inlay 두께는 2 mm로 하였으며, 배치된 셀 간의 간격은 2 mm, 셀과 프레임 간의 거리는 21 mm로 선정하였다2,14).
Table 1
Thickness of components in large-scale bifacial photovoltaic module
| Layer | Thickness (mm) |
| Glass | 3.2 |
| Solar cell | 0.18 |
| EVA + Solar Cell | 0.8 |
| Frame-inlay | 2.0 |
2.2 기계적 물성 및 유한요소 모델
대면적 양면형 태양광 모듈의 구성요소에 대한 각각의 기계적 물성은 Table 2와 같다. 훅의 법칙에 따른 등방성 재질의 텐서 표현은 식(1)과 같다. 본 연구에 적용된 실리콘 웨이퍼는 단결정 태양광 웨이퍼로 표면 법선이 <100>면을 따른다. 이때, 강성행렬은 식(2)와 같이 표현할 수 있으며, 본 연구에 적용된 각 계수 값은 C11 = 164.8 GPa, C12 = 63.5 GPa, C44 = 79.0 GPa이다15,16,17,18).
Table 2
Mechanical properties of components in large-scale bifacial photovoltaic module
| Material | Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s ratio |
| Glass | 2,500 | 70 | 0.2 |
| EVA | 0.96 | T-dep. | 0.4 |
| Solar cell (Silicon) | 2.329 | Stiffness matrix | |
| Frame (Al) | 2.7 | 70 | 0.33 |
| Frame-inlay | 0.067 | 0.0074 | 0.3 |
유한요소해석을 위한 태양광 모듈 mesh 모델링 단면은 Fig. 2와 같다. 요소는 8절점 6면체요소(C3D8)를 사용하였으며, 각 요소 간의 접촉은 미끄러짐 없이 완전히 접합된 것으로 가정하여 노드 결합으로 모사하였다.
2.3 경계조건
본 연구에서는 결정질 실리콘 태양전지 IEC 국제규격(IEC 61215)의 기계적 하중 시험 방법을 토대로 구조해석을 수행하였다. 기계적 하중 시험 방법에서는 풍속이 130 km/h일 때, 풍압을 대략 ±800 Pa에 상응한다고 가정하며, 안전계수 3을 적용해 2,400 Pa를 모듈 전면에 부과하도록 명시되어있다19).
Fig. 3는 본 연구에서 진행한 구조해석을 위한 경계조건을 나타내고 있다. 본 연구에 적용된 태양광 모듈의 구조 및 기계적 하중 시험에서 적용하는 하중 조건의 경우 YZ평면, XZ평면에 대해 각각 대칭인 형태이다. 이는 대칭 평면에 대해 분할하였을 때, 각 분할된 영역이 동일한 거동을 갖는 것을 의미하며, 분할된 하나의 영역에 대해 수치해석을 수행해 전체 문제에 해당하는 결과를 얻을 수 있다20). 이 경우 전체 모델을 해석하는 것에 비해 시간 및 자원을 절감할 수 있는 이점이 있다. 이러한 이점으로 태양광 모듈에 대해 유한요소해석을 수행한 선행 연구에서도 Symmetry 조건을 적용한 것을 확인하였다2,5,16,18). 따라서 본 연구에서도 Symmetry 조건을 적용하여 1/4 모델에 대해 구조해석을 수행하였다. 즉, YZ평면에 위치한 노드에 대해서는 x축 방향 변위, y축 모멘트, z축 모멘트가 발생하지 않도록 구속하여 YZ평면에 수직한 방향으로 노드가 이동할 수 없도록 하였다. 마찬가지로 XZ평면에 위치한 노드에 대해서는 y방향 변위, x축 모멘트, z축 모멘트가 발생하지 않도록 구속하여 대칭조건을 만족하도록 하였다. 하중조건으로는 중력에 의한 자중을 고려하였으며, 모듈 전면의 분포하중을 점진적으로 600 Pa까지 부과하였다. 구속 위치는 모듈 끝에서 모듈 길이의 약 20%의 위치에 볼트가 체결되는 부분으로 적용하였고7), Solver로는 ABAQUS를 사용하였다.
3. 실험 설계
3.1 실험계획법
태양광 모듈 알루미늄 프레임의 형상을 결정하는 인자 중 하중이 부과되었을 때 지지역할을 하는 인자를 확인하기 위해 기존 상용 알루미늄 프레임을 적용하여 구조해석을 수행하였다. 구조해석 결과에서 프레임에 응력이 집중되고 변형이 발생한 위치를 바탕으로 프레임 형상 인자를 Fig. 4와 같이 결정하였다. 프레임 형상 인자 5개에 대해 2수준으로 배치하여 총 32개의 실험계획을 수립하였으며, 사용된 인자들의 수준표는 Table 3와 같다.
4. 결과 및 고찰
4.1 구조해석 결과
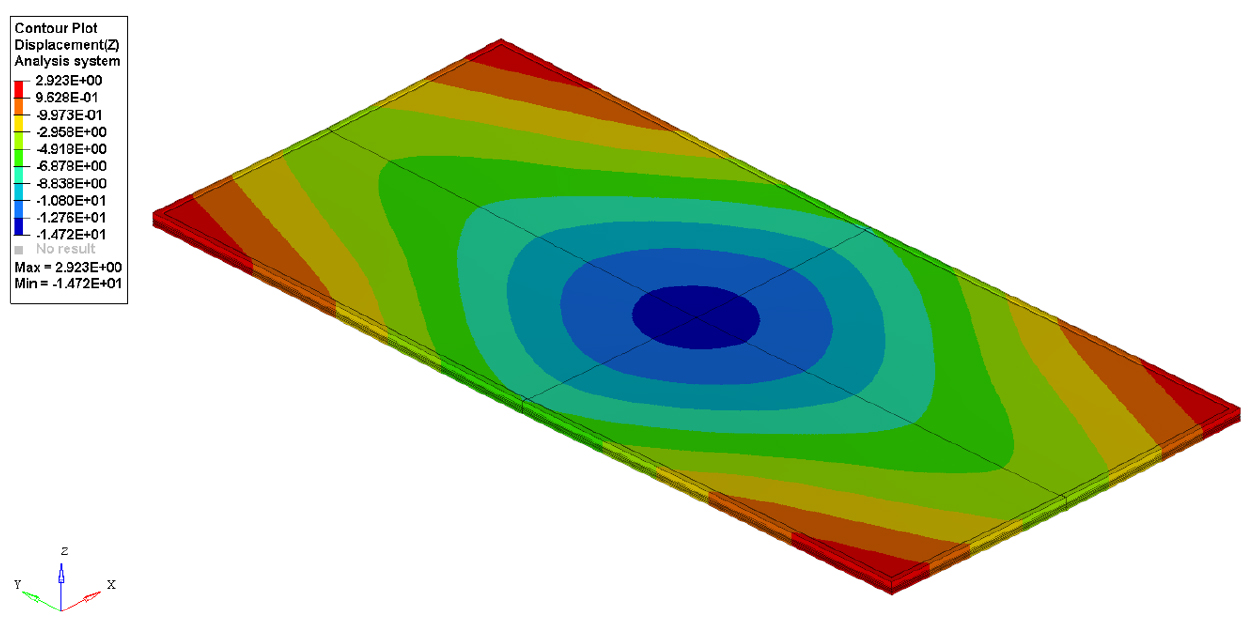
Fig. 5는 상용 알루미늄 프레임을 적용한 양면형 대면적 태양광 모듈의 구조해석 결과를 나타내고 있다. 해석 결과 최대 처짐은 모듈의 중앙에서 발생하였으며, 이는 기존의 태양광 모듈의 기계적 하중에 대한 연구결과와 동일한 거동임을 확인하였다2,5,6,16,17). 이때 최대 처짐량은 14.72 mm이며, 지지점을 기준으로 모듈의 끝 부분까지 처짐에 의한 반력으로 양의 방향 최대 약 2.40 mm까지 변위가 발생하였다.
Table 4는 32개의 실험계획에 대한 구조해석 결과 및 프레임 중량을 나타내고 있다. 최소 처짐은 28번 조건에 9.76 mm로 나타났으며, 기존 알루미늄 프레임을 적용했을 때보다 처짐이 약 33.7% 감소하였다. 이때 프레임 무게는 4.03 kg으로 약 24.7% 증가하였다.
Table 4
Deflection and frame weight of large-scale bifacial PV module by case
4.2 주효과도 분석
Fig. 6는 태양광 모듈 프레임에 하중이 부과되었을 때 발생하는 처짐에 대한 주효과도이다. 프레임 형상 인자 중 처짐에 가장 영향을 미치는 인자는 a로 나타났으며, a의 경우 두께가 증가함에 따라 하중에 의한 좌굴 현상이 줄어들어 처짐이 감소하는 것으로 판단된다. b의 경우 회전중심점 이동으로 인한 모멘트 감소로 처짐이 줄어드는 것으로 사료되며, d, e의 경우 두께 증가에 따른 강성 증가로 다소 영향을 끼치는 것으로 보인다. c의 경우 상대적으로 영향이 적은 것을 확인하였다.
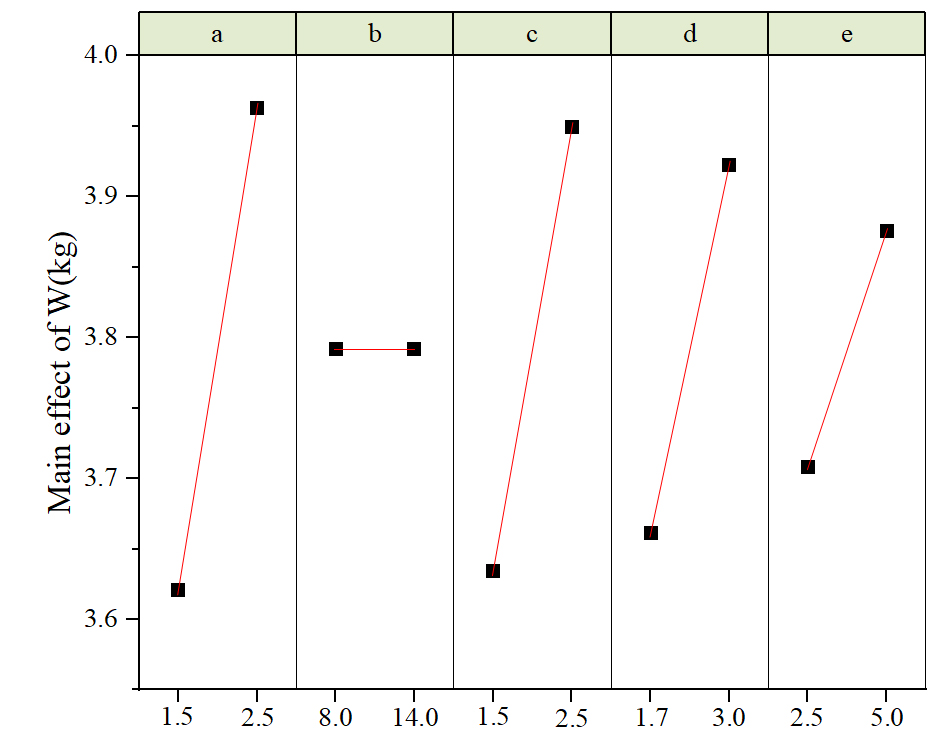
Fig. 7은 프레임 중량에 대한 주효과도이다. 두께를 증가하였을 때, 증가하는 면적이 큰 a, c, d가 가장 영향이 크게 나타났다. 상대적으로 면적이 작은 e는 다른 인자에 비해 영향이 작게 나타났으며, b의 경우 위치와 관련된 치수로 중량에 영향을 끼치지 않았다.
4.3 반응표면법을 이용한 분석
해석결과를 기반으로 반응표면법을 활용하여 처짐과 프레임 중량에 대한 회귀방정식을 도출하였으며, 이는 식(3), (4)와 같다. 처짐량(U)와 중량(W)의 회귀방정식에 대한 결정계수는 각각 0.96, 0.99로 인자 범위 내에서 비교적 정확하게 결과 값을 예측할 수 있을 것으로 판단하였다.
모듈에 과도하게 변위가 발생하면 셀이 파손되어 효율이 감소한다21). 프레임이 두꺼워지면 변위가 상대적으로 감소할 수 있으나, 제작비용이 증가한다. 따라서 확보한 회귀방정식을 토대로 반응표면법을 적용하여 처짐과 알루미늄 프레임 중량이 최소가 되는 최적인자를 도출하고자 하였다.
그 결과 최적의 값은 Fig. 8과 같이 a, b, c, d, e가 각각 1.904, 14.0, 1.5, 1.7, 2.5로 나타났다. Table 5는 기존프레임을 적용했을 때의 인자 수준과 반응표면법을 적용하여 도출한 최적 인자의 수준을 나타내고 있다. 치수는 제작공정을 고려해 소수점 첫째자리까지로 조정하였으며, 최적화 전후 프레임 형상은 Fig. 9과 같다.
최적화 과정은 인자 a가 주도하는 것으로 나타났다. a의 경우 처짐과 프레임 중량에 가장 큰 영향을 끼치는 인자로 두께가 늘어날 경우 처짐은 감소하지만 무게가 증가해, 두 결과를 보상하는 방향으로 최적인자가 도출되었다. b의 경우 중량에 대한 영향이 없고 길이가 길수록 처짐이 감소하므로 최댓값으로 도출되었으며 c, d, e의 경우 두께 증가에 따라 처짐에 대한 영향은 상대적으로 적으나 중량 증가에 비교적 큰 영향을 끼쳐 최솟값으로 도출되었다. 회귀식을 통해 계산된 처짐량은 11.1 mm이며, 무게는 3.37 kg으로 확인되었다.
Table 5
Levels of frame factors
| a | b | c | d | e | |
| Existing (mm) | 1.5 | 8.0 | 1.5 | 1.7 | 2.5 |
| Optimal (mm) | 1.9 | 14.0 | 1.5 | 1.7 | 2.5 |
4.4 최적화 모델 검증
회귀식을 통해 계산된 최적 인자로 태양광 모듈 프레임 설계 변경 후 구조해석을 수행하였다. 구조해석 결과 처짐량은 12.4 mm, 중량은 3.38 kg으로 나타났다. RSM 결과와 비교했을 때, 오차는 각각 10.3%, 0.1%로 나타났다.
Table 6는 기존 조건과 최적 조건의 처짐량과 중량을 나타내고 있다. 중량은 기존대비 0.15 kg 증가로 약 4.5% 증가했으며 기존 조건과 최적 조건의 해석결과를 비교했을 때, 처짐량은 기존대비 2.3 mm 감소로 약 15.8% 감소하는 것을 확인하였다.
5. 결 론
본 연구에서는 대면적 양면형 태양광 모듈 처짐 개선을 위해 유한요소해석과 반응표면법을 활용한 프레임 형상 최적화 방법을 기술하였으며, 그 결과를 요약하면 다음과 같다.
1) 구조해석결과 최대 처짐은 모듈의 중앙부에서 나타났다.
2) 주효과 분석 결과 프레임 형상 인자 중 처짐에 주로 영향을 미치는 인자는 a와 b로 나타났다. a의 경우 두께가 증가함에 따라 하중에 의한 좌굴 현상이 줄어들어 처짐이 감소하는 것으로 판단되며, b의 경우 회전중심점 이동으로 인한 모멘트 감소로 처짐이 줄어드는 것으로 사료된다.
3) 반응표면법을 활용하여 처짐량과 중량이 최소가 되는 최적인자를 도출한 결과 a, b, c, d, e가 각각 1.904 mm, 14.0 mm, 1.5 mm, 1.7 mm, 2.5 mm로 나타났다. 이때 중량은 3.37 kg, 처짐량은 11.1 mm로 나타났다.
4) 최적인자로 프레임 형상을 변경하여 구조해석을 수행한 결과 처짐량은 12.4 mm, 중량은 3.38 kg으로 RSM결과와의 오차는 각각 10.3%, 0.1%으로 확인되었다. 구조해석 결과를 기반으로 기존 조건과 최적 조건의 처짐량과 중량을 비교하면 중량은 기존대비 0.15 kg 증가로 약 4.5% 증가하였으며, 처짐량은 기존대비 2.3 mm 감소로 약 15.8% 감소하는 것을 확인하였다.
5) 결과적으로 대면적 양면형 태양광 모듈에 대해 기계적 하중 조건에서 유한 요소 모델을 개발하기 위한 방법론을 제시하였으며, 프레임 형상에 대한 최적화 방법을 기술하였다. 향후 이를 기반으로 모듈 강성 보강을 위한 각 소재별 두께, 물성 등의 최적 수준 도출에 활용할 수 있을 것으로 기대된다.