1. 서 론
2. 일사 품질관리
3. 직달 및 산란과 전일사 상관계수
3.1 산란과 전일사 상관관계
3.2 직달과 전일사 상관관계
4. 지역계수 및 모델성능 비교
4.1 산란과 전일사 상관관계 지역계수 및 모델성능
4.2 직달과 전일사 상관관계 지역계수 및 모델성능
5. 결 론
1. 서 론
수평면 전일사(Global horizontal irradiation, GHI)는 직달 및 산란 일사로 분리될 수 있는데 수평면 전일사의 경우는 많은 지역에서 측정되지만 수평면 산란 및 법선면 일사의 경우 측정이 용이하지 못하였다. 따라서 상대적으로 측정하기 용이한 수평면 전일사 데이터를 기반으로 수평면 직달 일사(Bean horizontal irradiation, BHI)와 산란 일사(Diffuse horizontal irradiation, DHI)를 분리하는 모델이 필요하였다. 직산분리로 얻어진 수평면 직달 일사를 이용하면 법선면 일사(Direct normal irradiation, DNI)를 구할 수 있는데 이것은 재생에너지 및 건물부하용 시뮬레이션의 표준기상자료에 필수적인 데이터로 사용된다. 한국태양에너지학회의 20년 표준기상데이터에서는 Lee et al. (2000)1)의 연구를 기반으로 국내기후와 유사한 Watanabe (1983)2) 모델 의 기존계수를 활용하여 산란 일사를 계산하였다. 이후 30년 표준기상데이터에서는 산란과 전일사 상관관계를 이용한 Orgill and Holland (1977)3) 모델 , Erbs et al. (1982)4) 모델 , Reindl et al. (1990)5) 모델 , CIBSE Guide J (2008)6) 모델의 기존계수를 활용하여 대전지역의 전일사 및 직달 일사 데이터와 비교하였고, 그중 최적의 성능을 보인 CIBSE Guide J 모델에 대전 지역계수를 산출하여 산란 일사 계산에 사용하였다. 산란 일사는 일사계(pyrheliometer)에 셰이드 링(shade ring)을 추가하여 측정된 데이터로 직달 일사와 비교하여 상대적으로 쉽게 얻을 수 있었지만, 최근 법선면 일사 측정이 용이해지면서 산란계수 및 직달계수를 위한 품질관리(Quality control)가 요청되고 있다.
따라서 본 연구에서는 대전지역 직달 및 산란과 전일사 상관계수를 고찰하기 위하여 5단계의 품질관리를 수행하고 , 국내에서 측정한 일사 데이터를 이용하여 기존의 산란과 전일사 상관계수 모델에 적용할 것이다. 또한 기존의 모델을 수정하여 직달과 전일사 상관관계 모델을 개발하고, 대전지역의 전일사 및 직달 일사 데이터를 활용하여 지역계수 및 허용범위 경계(Boundary of envelope of acceptance)에서의 대전지역계수를 제시할 것이다. 이러한 과정을 통하여 기존계수, 지역계수 및 허용범위 경계에서의 지역계수를 이용한 직달 및 산란과 전일사 상관계수 모델의 성능을 비교하고, 대전지역에 적합한 모델을 고찰할 것이다.
2. 일사 품질관리
일사 데이터는 종종 데이터가 공개되기 전에 사전 품질 검사를 수행하여 오류가 있거나 의심스러운 값을 수정되어야 한다. 컴퓨터 시뮬레이션을 위한 누락 없는 연속적인 데이터 세트를 생성하기 위해서는 확립 된 절차와 명시적으로 개발 된 추가 방법을 사용하여 채워져야 한다. Muneer and Fairooz (2002)7)는 파일에서 불필요한 기상 데이터를 제거하고 전일사 및 산란 일사에 대한 모호하고 누락 된 값을 제거하였다. Younes et al. (2005)8)는 일사량 데이터의 품질평가를 위한 현재 가능한 절차를 검토했다. Lee et al. (2013)9)는 7대 광역시 전일사의 품질에 대한 일련의 품질검사를 실시하였다. 본 연구에서는 한국태양에너지학회의 표준기상데이터를 위하여 한국에너지기술연구원의 협조를 얻어 입수한 대전 측정 전일사 및 직달 일사 데이터(2011.1-2012.12)를 이용하여 다음과 같은 5단계의 일사 품질관리(Solar irradiation quality control)를 사용하였다. 1, 2, 3단계는 일반적인 일사(수평면 전일사, 법선면 일사, 산란 일사)에 대한 품질관리 이지만, 4, 5단계는 청명계수와 산란계수 및 직달계수를 위한 품질관리이다. 2013년 선행연구의 일사 품질관리는 1, 2, 3단계로 수행하였지만, 본 연구에서는 4, 5단계의 품질관리를 추가로 수행하였다.
1단계 : 누락된 데이터에 대한 품질관리
•누락된 시간별 일사 데이터
2단계 : 대기권 밖 수평면 일사(I0h)와의 비교에 의한 품질관리
•대기권 밖 수평면 일사(I0h) 보다 1,2 배 큰 수평면 전일사(Igh) 시간별 데이터
•대기권 밖 수평면 일사(I0h) 보다 큰 수평면 산란 일사(Idh) 시간별 데이터
•대기권 밖 수평면 일사(I0h) 보다 0.8배 큰 수평면 직달 일사(Ibh) 시간별 데이터
3단계 : 태양고도(h)에 의한 품질관리
•태양 고도(h)가 5°미만인 시간별 데이터
4단계 : 수평면 전일사(Igh)와의 비교에 의한 품질관리
•수평면 전일사(Igh) 보다 배 큰 수평면 산란 일사(Idh) 시간별 데이터
•수평면 전일사(Igh) 보다 배 큰 수평면 직달 일사(Ibh) 시간별 데이터
5단계 : 허용범위의 경계에 의한 품질관리
•청명계수-산란계수(kt-kd) 좌표에 의한 허용범위의 경계 설정
•청명계수-직달계수(kt-kb) 좌표에 의한 허용범위의 경계 설정
허용범위의 경계는 청명계수와 산란계수 및 직달계수의 값에서 오차범위를 제외한 경계로 설정되고, 청명계수(kt)와 산란계수(kd) 및 직달계수(kb)는 다음 식과 같다.
| $$k_t=I_{gh}/(I_o\times sinh)=I_{gh}/I_{oh}$$ | (1) |
| $$k_d=I_{dh}/I_{gh}$$ | (2) |
| $$k_b=(I_{bn}\times sinh)/I_{gh}=I_{bh}/I_{gh}$$ | (3) |
영국의 청명계수-산란계수(kt-kd) 좌표에 대한 허용범위의 경계7)는 다음과 같다.
영국(UK) : (0,1), (0.5,1), (1,0.14), (1,0), (0.8,0), (0.2,0.9), (0,0.9), 및 (0,1)
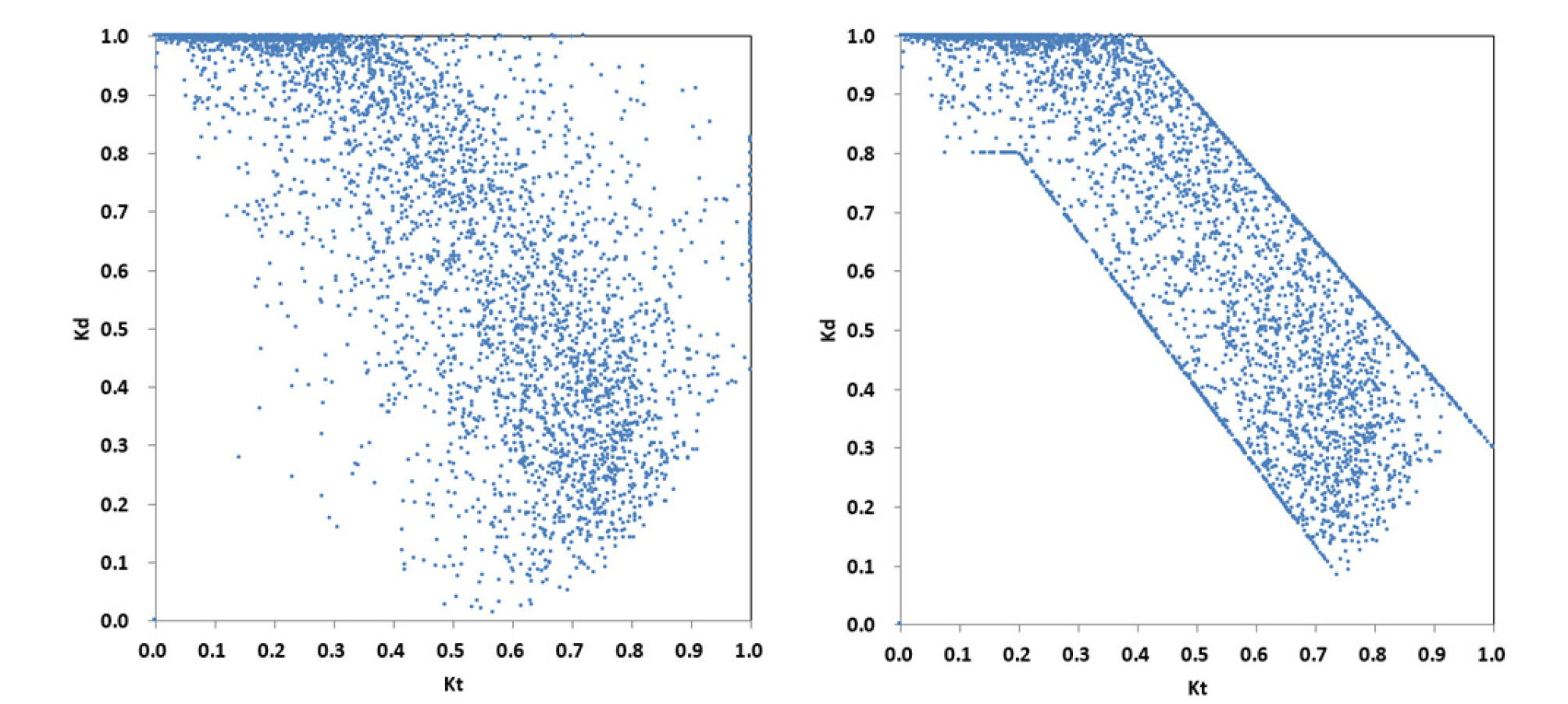
대전지역 청명계수-산란계수(kt-kd) 좌표 에 대한 허용범위의 경계는 Fig. 1와 같고, 대전의 허용범위의 경계가 영국보다 조금 확장되었다. 따라서 대전지역뿐만 아니라 우리나라 전역에 대한 허용범위의 경계의 성정이 요청된다.
대전(Daejeon) : (0,1), (0.4,1), (1,0.3), (1,0), (0.8,0), (0.2,0.8), (0,0.8), 및 (0,1)
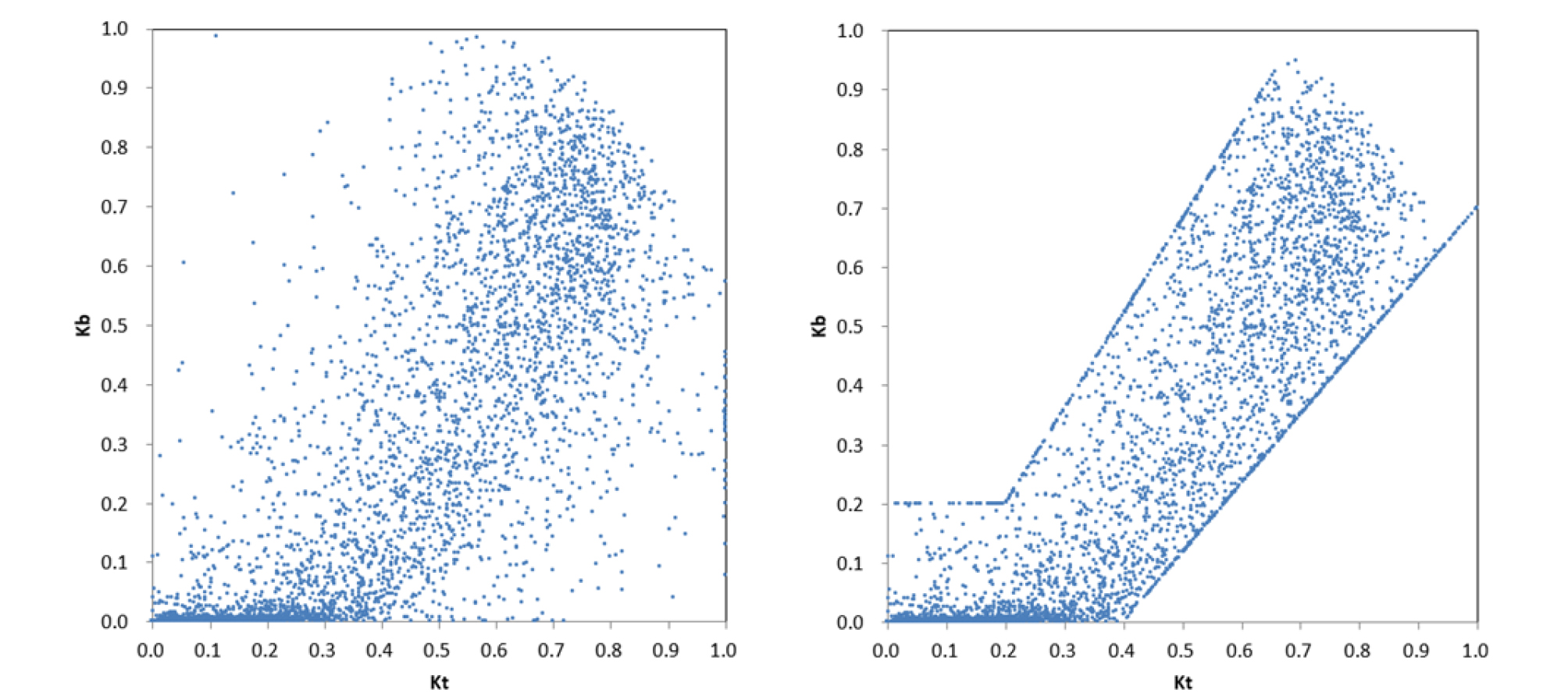
대전지역 청명계수-직달계수(kt-kb) 좌표 에 대한 허용범위의 경계는 다음과 같다(Fig. 2 참조).
대전(Daejeon) : (0,0), (0.4,0), (1,0.7), (1,0), (0.7,1), (0.2,0.2), (0,0.2), 및 (0,0)
3. 직달 및 산란과 전일사 상관계수
3.1 산란과 전일사 상관관계
산란 일사는 일사계에 셰이드 링을 추가하여 측정된 데이터로 직달 일사와 비교하여 상대적으로 쉽게 얻을 수 있었다. 본 연구는 산란과 전일사 상관관계 모델 중에서 1차방정식의 Orgill and Holland (1977) 모델, 3차방정식의 CIBSE Guide J (2008) 모델 및 4차방정식의 Erbs et al. (1982) 모델에 대하여 고찰하였다. Orgill and Holland 모델은 수평면의 전일사 및 산란 일사의 시간당 비율을 결정하는 최초의 방정식이었다. 산란과 전일사의 상관관계는 다음 식과 같다.
| $$k_d=1.0-0.249\;k_t,\;k_t\;<\;0.35$$ | (4) |
| $$k_d=1.577-1.84\;k_t,\;0.35\;\leq\;k_t\;\leq\;0.75$$ | (5) |
| $$k_d=0.177,\;k_t\;>\;0.75$$ | (6) |
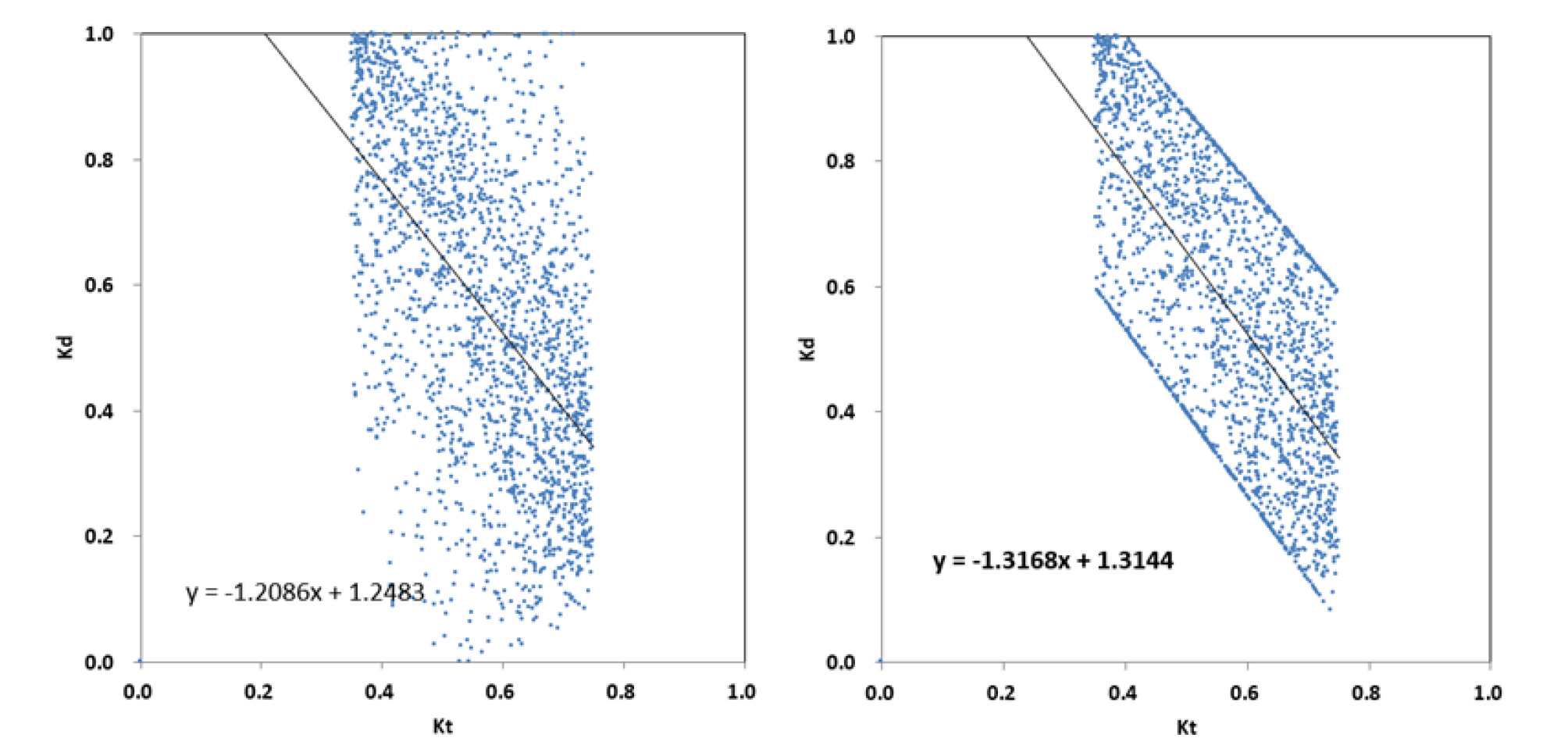
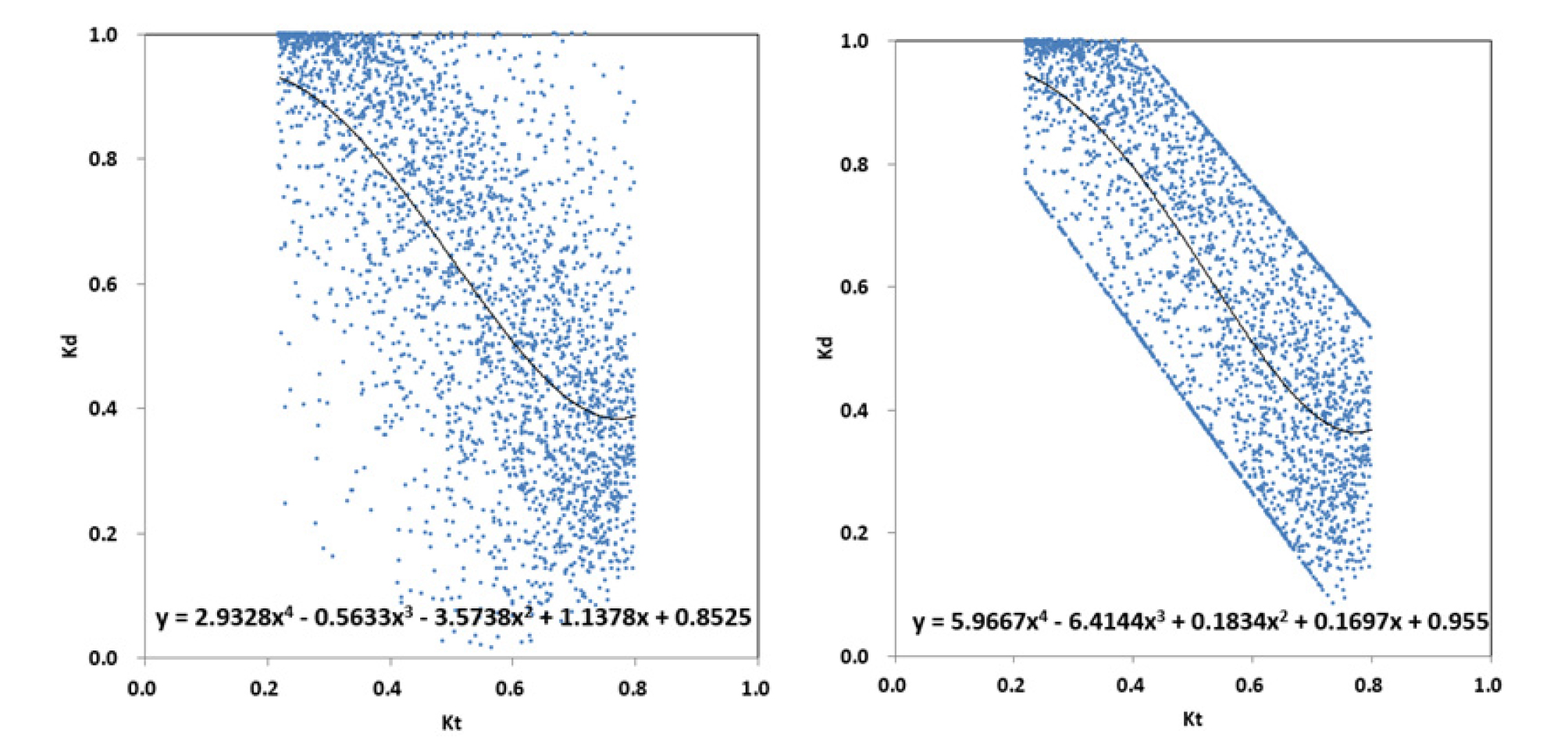
일사 품질관리 4, 5단계를 거쳐 대전지역의 산란과 전일사 상관관계의 허용범위 경계는 Fig. 1과 같이 선정되고, 2개의 지역계수를 위한 대전지역 청명계수-산달계수(kt-kd) 좌표는 Fig. 3과 같다.
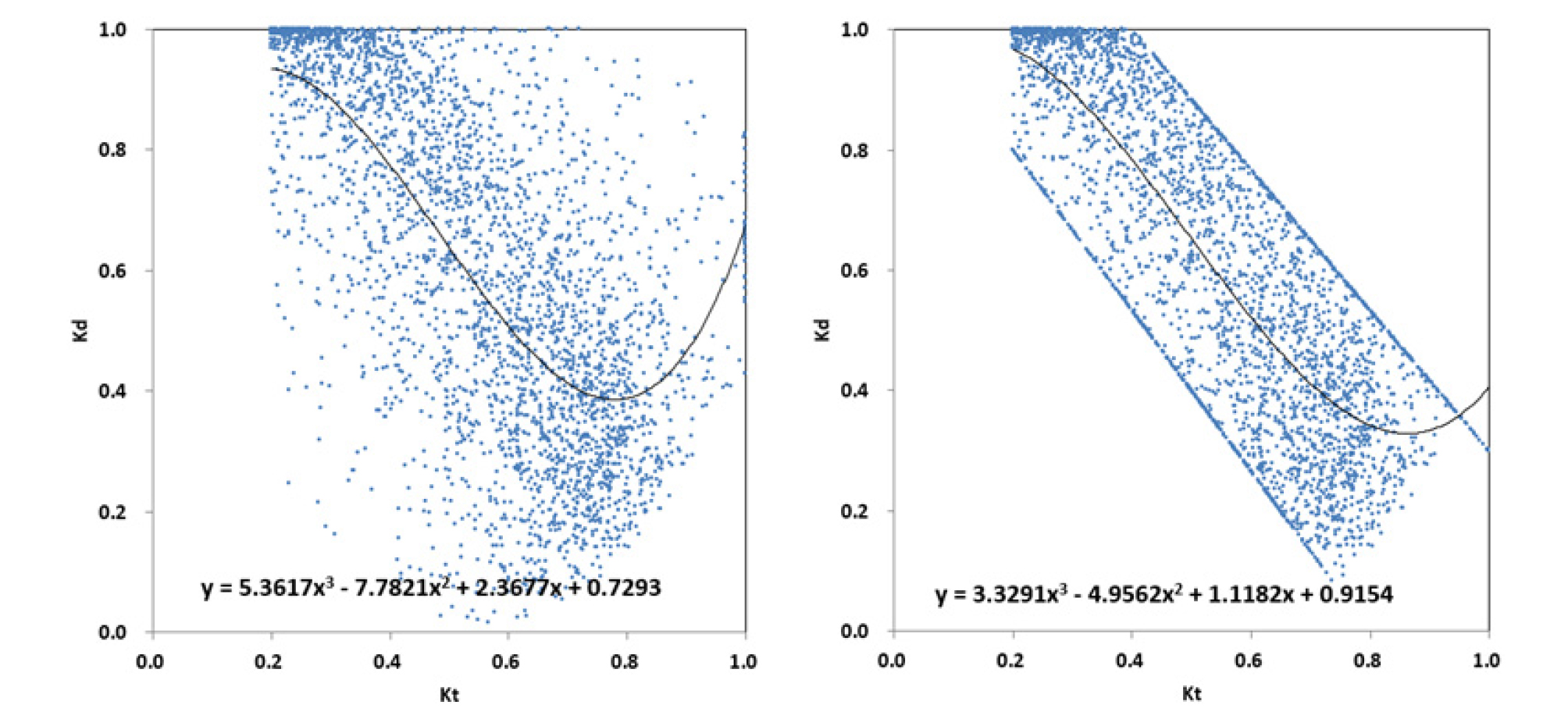
CIBSE Guilde J 모델은 시간당 수평면의 전일사를 이용하여 시간당 수평면 산란 일사를 평가하는 방정식을 제안하였다. 산란과 전일사의 상관관계는 다음 식과 같고, 2개의 지역계수를 위한 대전지역 청명계수-산달계수(kt-kd) 좌표는 Fig. 4와 같다.
| $$k_d=0.687+2.932k_t-8.546k_t^2+5.227k_t^3,\;k_t\;>\;0.2$$ | (7) |
| $$k_d=0.98,\;k_t\;\leq\;0.2$$ | (8) |
Erbs et al. 모델은 미국의 4지역에서 수평면의 전일사 및 산란 일사간의 연관성을 도출하였다. 산란과 전일사의 상관관계는 다음 식과 같고, 2개의 지역계수를 위한 대전지역 청명계수-산달계수(kt-kd) 좌표는 Fig. 5와 같다.
| $$k_d=1.0-0.09\;k_t,\;k_t\;\leq\;0.22$$ | (9) |
| $$k_d=0.9511-0.1604k_t+4.388k_t^2-16.638k_t^3+12.336k_t^4,\;0.22\;<\;k_t\;\leq\;0.8$$ | (10) |
| $$k_d=0.165,\;k_t\;>\;0.8$$ | (11) |
3.2 직달과 전일사 상관관계
직산분리 모델 중 직달과 전일사 상관관계는 법선면 일사 측정의 어려움 때문에 널리 이용되지 못했지만, 최근 법선면 일사 측정이 용이해지면서 상관관계의 모델이 요청되고 있다. 본 연구에서는 대전지역의 전일사 및 직달 일사를 이용하여 1차방정식의 수정 Orgill and Holland 모델, 3차방정식의 수정 CIBSE Guide J 모델 및 4차방정식의 수정 Erbs et al. 모델을 도출하였다. 대전지역의 지역계수를 고려한 수정 Orgill and Holland 모델의 직달과 전일사 상관관계는 다음 식과 같다.
| $$k_b=-0.0003+0.3747\;k_t,\;k_t\;<\;0.35$$ | (12) |
| $$k_b=-0.2482+1.2085\;k_t,\;0.35\;\leq\;k_{t\;}\leq\;0.75$$ | (13) |
| $$k_b=0.58,\;k_t\;>\;0.75$$ | (14) |
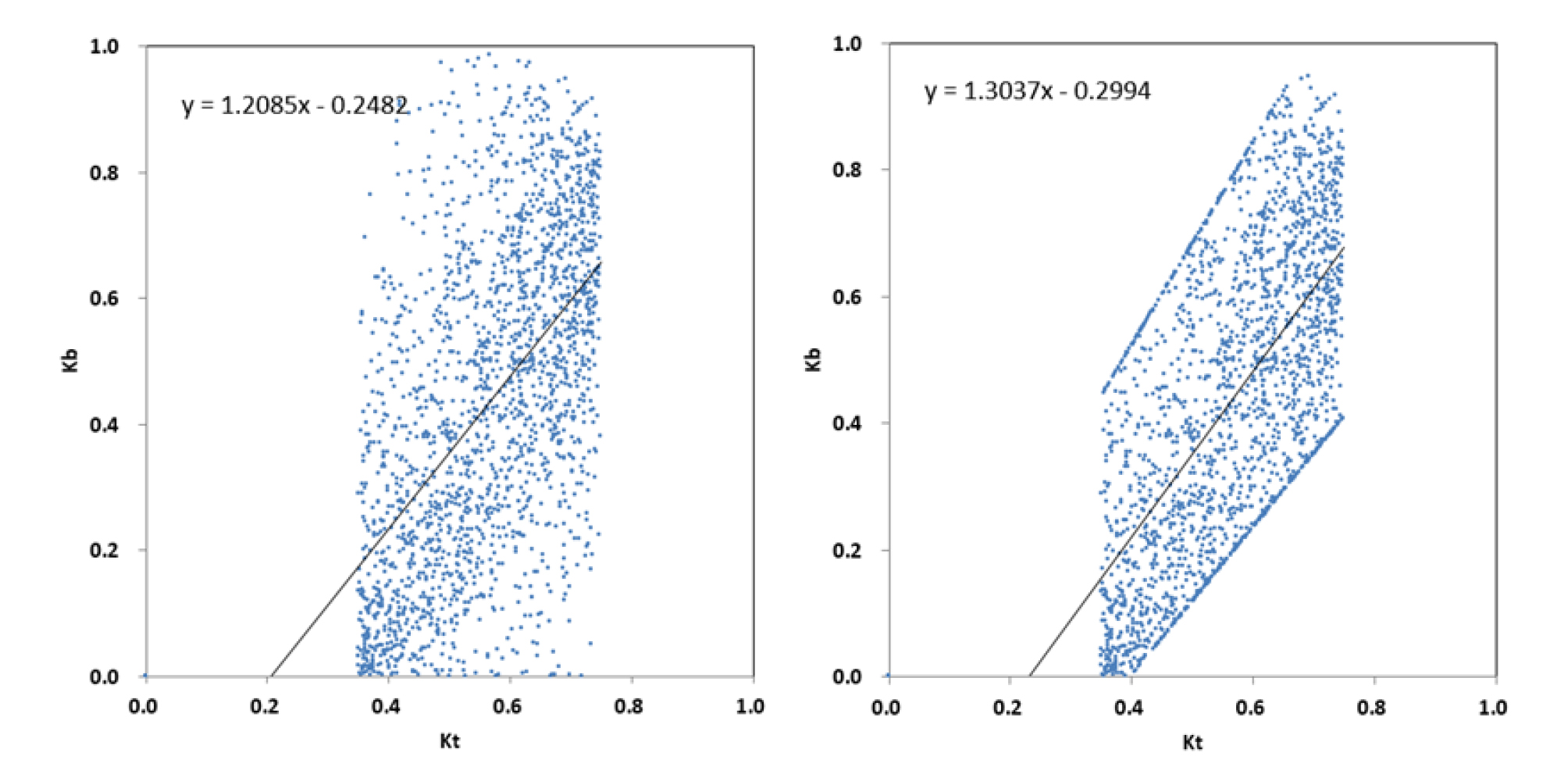
일사 품질관리 4, 5단계를 거쳐 대전지역의 직달과 전일사 상관관계의 허용범위 경계가 Fig. 2와 같이 선정되고, 2개의 지역계수를 위한 대전지역 청명계수-직달계수(kt-kb) 좌표는 Fig. 6과 같다.
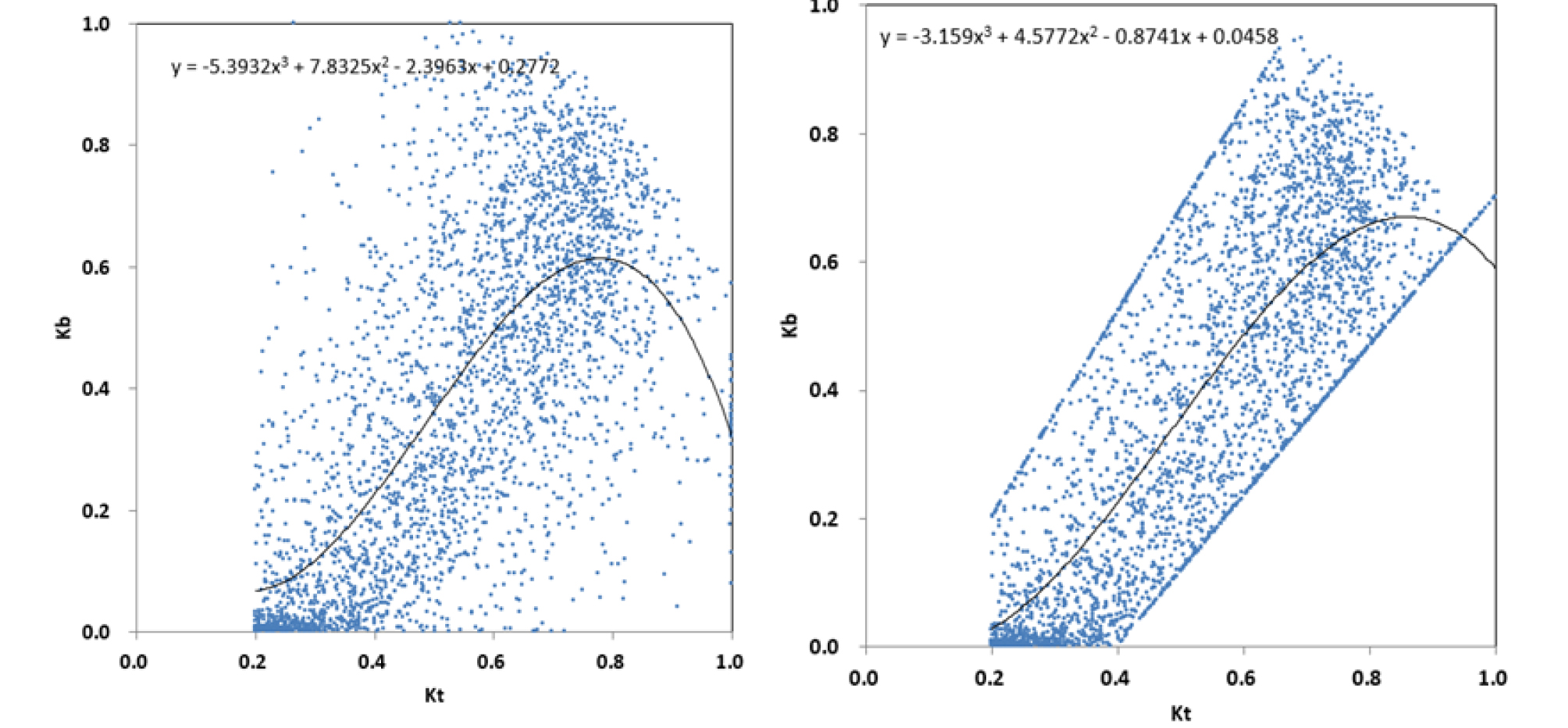
대전지역의 지역계수를 고려한 수정 CIBSE Guilde J 모델의 직달과 전일사 상관관계는 다음 식과 같다. 2개의 지역계수를 위한 대전지역 청명계수-직달계수(kt-kb) 좌표는 Fig. 7과 같다.
| $$k_b=0.2772-2.3963\;k_t+7.8325\;k_t^2+5.3932\;k_t^3,\;k_t\;>\;0.2$$ | (15) |
| $$k_b=0.0239,\;k_t\;\leq\;0.2$$ | (16) |
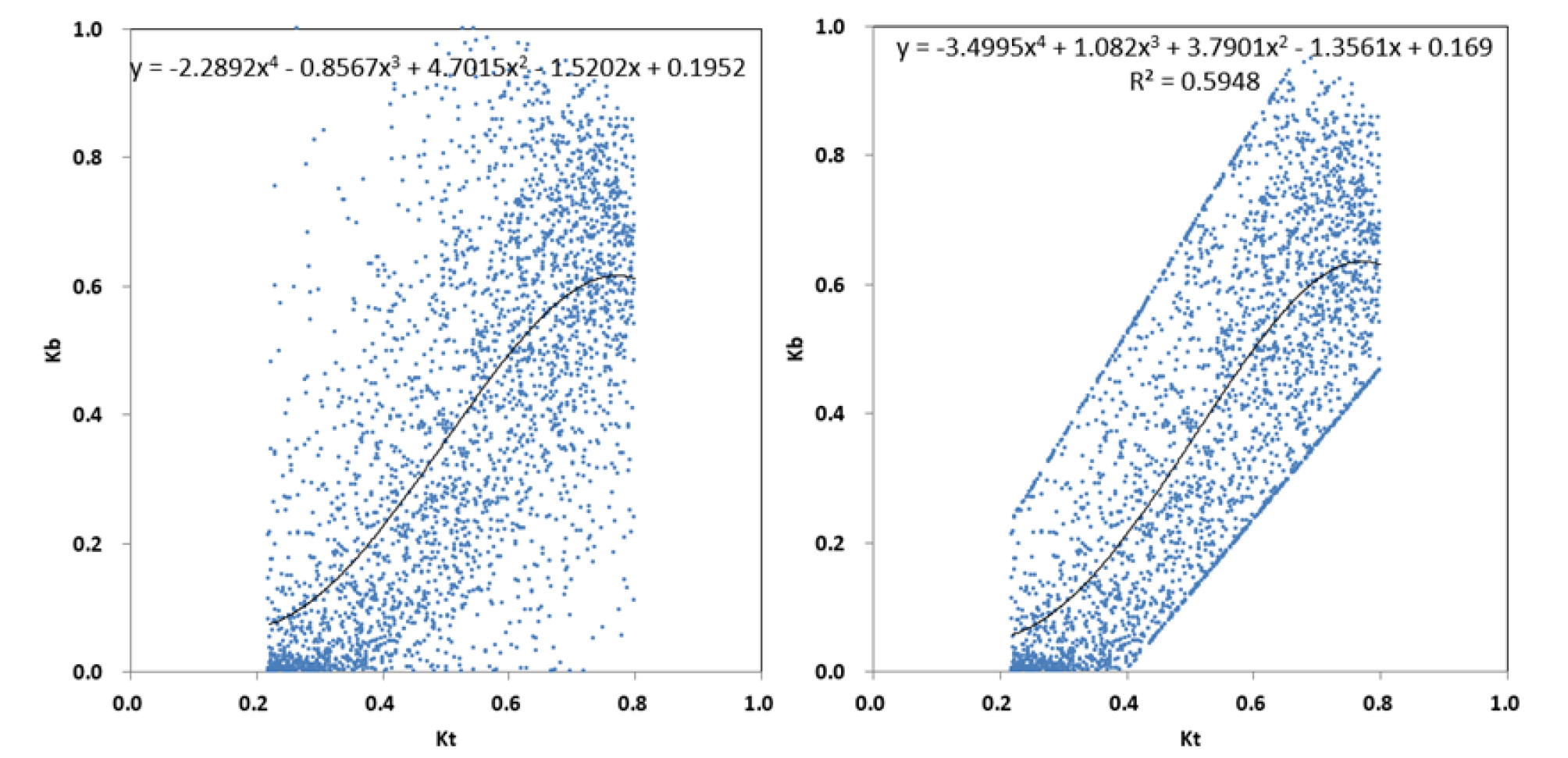
대전지역의 지역계수를 고려한 수정 Erbs et al. 모델의 직달과 전일사 상관관계는 다음 식과 같다. 2개의 지역계수를 위한 대전지역 청명계수-직달계수(kt-kb) 좌표는 Fig. 8과 같다.
| $$k_b=0.0231+0.1299\;k_t,\;k_t\;\leq\;0.22$$ | (17) |
| $$k_b=0.1952-1.5202\;k_t+4.7015\;k_t^2-8.567\;k_t^3-2.2892\;k_t^4,\;0.22\;<\;k_t\;\leq\;0.8$$ | (18) |
| $$k_b=0.54,\;k_t\;>\;0.8$$ | (19) |
4. 지역계수 및 모델성능 비교
4.1 산란과 전일사 상관관계 지역계수 및 모델성능
본 연구에서 사용된 계수들은 원 모델의 기존 계수, 대전지역의 측정 데이터를 이용해 도출된 지역계수 및 대전지역의 허용범위 경계에서 도출된 지역계수로 구분할 수 있다. Tables 1, 2, 3은 각 모델에서 기존 계수와 새로 도출된 계수(지역계수 및 허용범위 경계에서의 지역계수)를 보여주고 있다.
Table 1 Site-fitted coefficient of Daejeon by Orgill and Holland Model for kt-kd
Table 2 Site-fitted coefficient of Daejeon by CIBSE Guide J Model for kt-kd
Table 3 Site-fitted coefficient of Daejeon by Erbs et al. Model for kt-kd
기존 계수, 지역계수 및 허용범위 경계에서의 지역계수간의 차이를 비교하면, Erbs et al. 모델이 가장 켰고, Orgill and Holland 모델이 가장 적었다. 방정식의 차수가 증대함으로써 이러한 차이가 증대됨을 고려하면 CIBSE Guilde J 모델은 상대적으로 가장 차이가 적었다.
Table 4는 각 모델에서 기존 계수와 새로 도출된 계수(지역계수 및 허용범위 경계에서의 지역계수)의 모델 성능을 MBE, RMSE, r2로 비교한 것이다. 기존 계수와 2개의 지역계수를 적용한 모델들의 성능을 비교해 보면, MBE, RMSE, r2가 각각 14.91에서 –3.02로, 48.95에서 35.69로, 0.62에서 0.69로 상당한 수준으로 개선되었다. 기존 및 대전의 지역계수를 적용한 모델 중에서는 CIBSE Guilde J 모델이 가장 높은 성능을 보였고, 허용범위 경계에서의 대전의 지역계수를 적용한 경우 Erbs et al. 모델이 가장 최고의 성능을 보여주었다.
Table 4 Comparison of Estimation results of diffuse to global solar irradiation correlation coefficients models for Daejeon
4.2 직달과 전일사 상관관계 지역계수 및 모델성능
Tables 5, 6, 7은 각 모델에서 기존 계수와 새로 도출된 계수(지역계수 및 허용범위 경계에서의 지역계수)를 보여주고 있다. 대전의 지역계수 및 허용범위 경계에서의 지역계수간의 상관계수의 차이를 비교하면, 산란과 전일사 상관관계 모델과 유사하게 수정 Erbs et al. 모델이 가장 켰고, 수정 Orgill and Holland 모델이 가장 적었다.
Table 5 Site-fitted coefficient of Daejeon by modified Orgill and Holland Model for kt-kb
Table 6 Site-fitted coefficient of Daejeon by modified CIBSE Guide J Model for kt-kb
| Class | a | x | x^2 | x^3 | |
| Daejeon site-fitting | 0.2 < kt ≤1.0 | 0.2772 | -2.3963 | 7.8325 | -5.3932 |
| 0.00 < kt ≤ 0.2 | 0.0384 | ||||
|
Daejeon boundary site-fitting | 0.2 < kt ≤1.0 | 0.0458 | -0.8741 | 4.5772 | -3.1590 |
| 0.00 < kt ≤ 0.2 | 0.0239 | ||||
Table 7 Site-fitted coefficient of Daejeon by modified Erbs et al. Model for kt-kb
Table 8은 각 모델에서 지역계수 및 허용범위 경계에서의 지역계수의 모델 성능을 MBE, RMSE, r2로 비교한 것이다. 2개의 지역계수를 적용한 모델들의 성능을 비교해 보면, MBE, RMSE, r2가 각각 5.70에서 2.53로, 46.13에서 42.65로, 0.88에서 0.89로 개선되었다. 지역계수를 적용한 모델 중에서는 수정 CIBSE Guilde J 모델이 가장 높은 성능을 보였고, 허용범위 경계에서의 대전 지역계수를 적용한 경우 수정 Orgill and Holland 모델이 가장 최고의 성능을 보여주었다. 이러한 성능의 결과는 산란과 전일사 상관관계 모델과 차이가 있었다. 따라서 측정 데이터가 전일사 및 산란 일사의 경우에는 산란과 전일사 상관관계 모델을 적용하고, 전일사 및 직달 일사의 경우에는 직달과 전일사 상관관계 모델을 적용하는 것이 요청된다.
Table 8 Comparison of Estimation results of beam to global solar irradiation correlation coefficients models for Daejeon
5. 결 론
대전지역의 측정 전일사 및 직달 일사 데이터를 활용하여 직달 및 산란 과 전일사 상관계수를 고찰하고, 성능을 비교분석한 결과는 다음과 같다.
(1)본 연구를 통하여 5단계의 일사 품질관리, 대전지역의 허용범위 경계, 2개의 지역계수(Fig. 1-6) 및 직달 및 전일사 상관계수 모델을 제시하였다.
(2)기존, 지역계수 및 허용범위 경계에서의 지역계수간의 차이를 비교하면, Erbs et al. 모델과 수정 Erbs et al. 모델이 가장 켰고, Orgill and Holland 모델과 수정 Orgill and Holland 모델이 가장 적었다. 방정식의 치수가 증대함으로써 이러한 차이가 증대됨을 고려하면 CIBSE Guilde J 모델은 상대적으로 차이가 적었다.
(3)산란 및 전일사 상관관계의 기존 및 대전 지역계수를 적용한 모델 중에서는 CIBSE Guilde J 모델이 가장 높은 성능을 보였고, 허용범위 경계에서의 대전 지역계수를 적용한 경우 Erbs et al. 모델이 가장 최고의 성능을 보여주었다.
(4)직달 및 전일사 상관계수 모델에서 지역계수 및 허용범위 경계에서의 지역계수의 성능을 비교하면 각각 수정 CIBSE Guilde J 모델과 Orgill and Holland 모델이 가장 최고의 성능을 보여주었다.
(5)직달 및 산란 과 전일사 상관계수 모델의 성능을 비교한 결과 최적 모델의 차이를 보였다. 따라서 측정 데이터에 따라 상관관계 모델을 적용하는 것이 요청된다.
기존계수, 지역계수 및 허용범위 경계에서의 성능을 비교하면, 허용범위 경계에서의 대전 지역계수를 적용한 모델들이 모두 최고의 성능을 보였으므로 대전지역뿐만 아니라 우리나라 전역에 대한 허용범위의 경계가 요청된다. 또한 본 연구는 직산분리 모델 중 직달 및 산란 과 전일사 상관계수를 이용한 모델에 대한 연구로 태양고도, 일조시간 및 운량 등을 포함한 모델에 대하여 추가연구가 요청된다.
기호설명
I0 : 태양상수 (1367 W/m2)
I0h : 대기권 밖 수평면 일사 (W/m2)
Idn : 법선면 일사 (direct nornal irradiation, DNI, W/m2)
Igh : 수평면 전일사 (global horizontal irradiation, GHI, W/m2)
Idh : 수평면 산란 일사 (diffuse horizontal irradiation, DHI, W/m2)
Ibh : 수평면 직달 일사 (beam horizontal irradiation, BHI, W/m2)
kt : 청명계수 (0~1)
kd : 산란계수 (0~1)
kb : 직달계수 (0~1)
h : 태양고도 (Degree)